A Complete Information To Quantity Techniques: Exploring The World Of Numbers

A Complete Information to Quantity Techniques: Exploring the World of Numbers

Associated Articles: A Complete Information to Quantity Techniques: Exploring the World of Numbers

Introduction

On this auspicious event, we’re delighted to delve into the intriguing subject associated to A Complete Information to Quantity Techniques: Exploring the World of Numbers. Let’s weave attention-grabbing data and provide contemporary views to the readers.

A Complete Information to Quantity Techniques: Exploring the World of Numbers

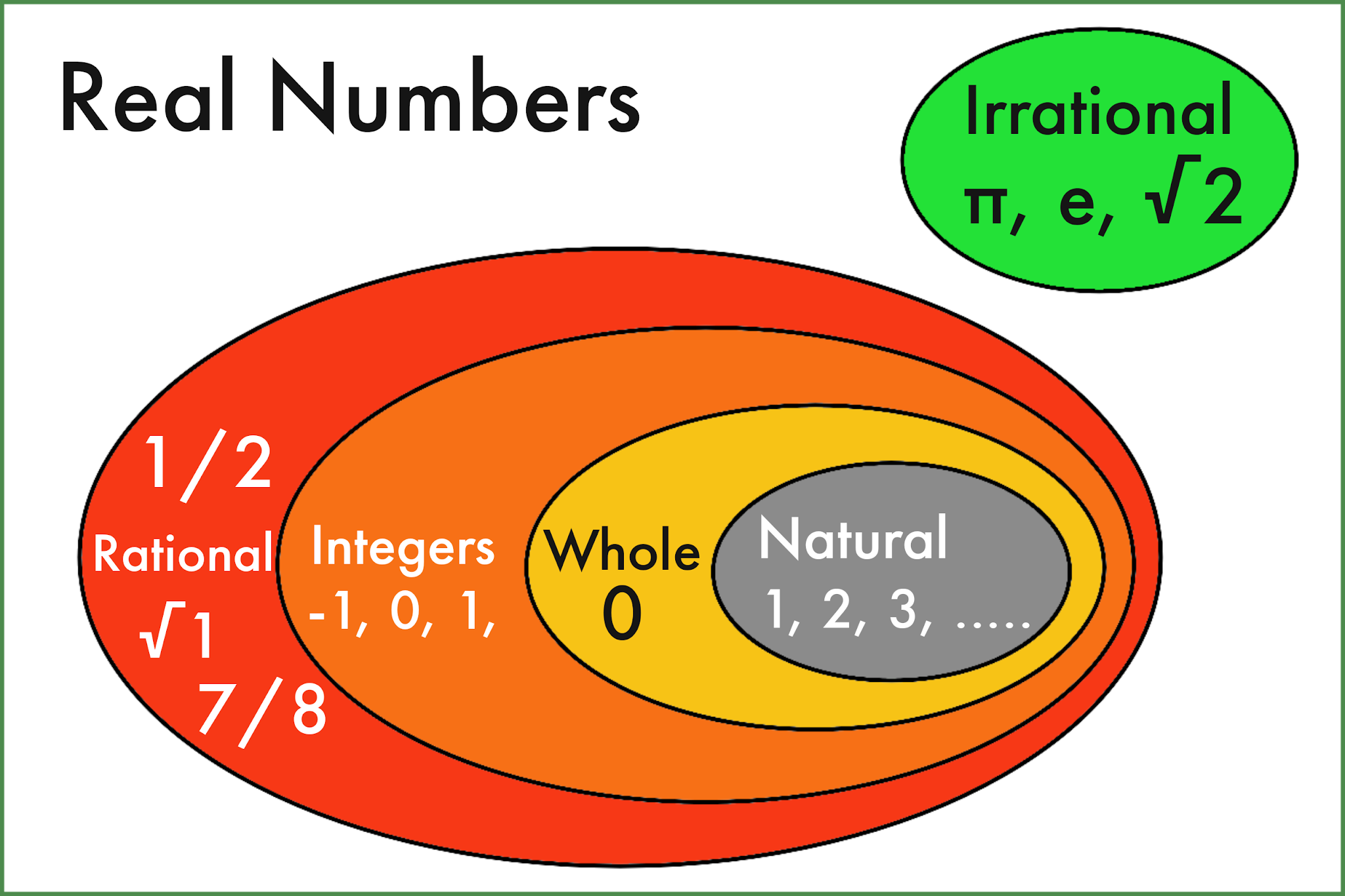
Numbers are the elemental constructing blocks of arithmetic, forming the bedrock upon which all quantitative reasoning is constructed. Nevertheless, the world of numbers is much richer and extra various than the straightforward integers we encounter in on a regular basis life. This text explores the assorted varieties of numbers, categorizing them and explaining their properties, finally offering a complete chart summarizing the relationships between these totally different quantity units.

1. Pure Numbers (Counting Numbers):

The only and most intuitive kind of quantity is the pure quantity. These are the numbers we use for counting objects: 1, 2, 3, 4, and so forth. They’re constructive entire numbers, excluding zero. The set of pure numbers is denoted by ℕ. Pure numbers are basic to arithmetic and type the idea for a lot of different quantity techniques. They’re utilized in just about each side of our every day lives, from counting apples to measuring distances. Operations like addition and multiplication are closed inside the pure numbers (which means the results of these operations on pure numbers is all the time one other pure quantity), however subtraction and division usually are not (e.g., 2 – 5 will not be a pure quantity).

2. Entire Numbers:

Entire numbers lengthen the set of pure numbers by together with zero. They’re the non-negative integers: 0, 1, 2, 3, and so forth. The set of entire numbers is often denoted by ℤ₀ or ℕ₀. The inclusion of zero permits for representing the absence of amount, a vital idea in lots of mathematical and real-world contexts. Like pure numbers, addition and multiplication are closed inside the entire numbers, whereas subtraction and division usually are not all the time closed.

3. Integers:

Integers embody each constructive and destructive entire numbers, together with zero. They’re represented by the set ℤ: …, -3, -2, -1, 0, 1, 2, 3, … Integers permit us to signify portions which can be lower than zero, which is important for representing ideas like debt, temperature beneath freezing, or modifications in altitude. The introduction of destructive numbers expands the scope of arithmetic, making subtraction a closed operation inside the integers. Nevertheless, division stays an open operation; dividing two integers doesn’t all the time end in an integer.

4. Rational Numbers:

Rational numbers are numbers that may be expressed as a fraction p/q, the place p and q are integers, and q will not be zero. This set is denoted by ℚ. Rational numbers embrace all integers (since any integer could be expressed as a fraction with a denominator of 1) and lots of different numbers like 1/2, 3/4, -2/5, and so forth. Rational numbers signify portions that may be exactly divided into equal elements. Decimal representations of rational numbers both terminate (e.g., 1/4 = 0.25) or repeat (e.g., 1/3 = 0.333…). The operations of addition, subtraction, multiplication, and division (excluding division by zero) are closed inside the rational numbers.

5. Irrational Numbers:

Irrational numbers are numbers that can not be expressed as a fraction of two integers. Their decimal representations are non-terminating and non-repeating. Well-known examples embrace π (pi), the ratio of a circle’s circumference to its diameter, and e (Euler’s quantity), the bottom of pure logarithms. √2 (the sq. root of two) is one other instance; it can’t be expressed as a fraction of two integers. Irrational numbers considerably increase the realm of numbers past the realm of fractions. The inclusion of irrational numbers is essential for superior arithmetic, notably in geometry and calculus.

6. Actual Numbers:

Actual numbers embody each rational and irrational numbers. They signify all factors on the quantity line. The set of actual numbers is denoted by ℝ. Actual numbers are used extensively in numerous fields, together with physics, engineering, and finance, to mannequin steady portions like temperature, distance, and time. All of the arithmetic operations are outlined for actual numbers (excluding division by zero).

7. Advanced Numbers:

Advanced numbers lengthen the actual quantity system by introducing the imaginary unit, denoted by i, the place i² = -1. A fancy quantity is expressed within the type a + bi, the place a and b are actual numbers. ‘a’ known as the actual half, and ‘b’ known as the imaginary half. Advanced numbers are essential in numerous areas of arithmetic, physics, and engineering, particularly in coping with equations that don’t have any actual options. As an illustration, the equation x² + 1 = 0 has no actual options however has two complicated options: x = i and x = -i. The set of complicated numbers is denoted by ℂ.

8. Transcendental Numbers:

Transcendental numbers are a subset of irrational numbers that aren’t the basis of any non-zero polynomial equation with rational coefficients. In easier phrases, they can’t be expressed as options to polynomial equations with rational numbers. π and e are examples of transcendental numbers. The examine of transcendental numbers is a fancy space of quantity idea.

9. Algebraic Numbers:

Algebraic numbers are numbers which can be roots of non-zero polynomial equations with rational coefficients. This set consists of all rational numbers (since they’re roots of linear equations) and lots of irrational numbers, equivalent to √2 (root of x² – 2 = 0). Transcendental numbers usually are not algebraic.

Abstract Chart:

Quantity System	Image	Description	Examples	Subsets of	Supersets of
Pure Numbers	ℕ	Constructive entire numbers	1, 2, 3, …		Entire Numbers, Integers, Rational Numbers, Actual Numbers, Advanced Numbers
Entire Numbers	ℤ₀ or ℕ₀	Non-negative integers	0, 1, 2, 3, …	Pure Numbers	Integers, Rational Numbers, Actual Numbers, Advanced Numbers
Integers	ℤ	Constructive, destructive, and nil entire numbers	…, -2, -1, 0, 1, 2, …	Pure Numbers, Entire Numbers	Rational Numbers, Actual Numbers, Advanced Numbers
Rational Numbers	ℚ	Numbers expressible as p/q (p, q integers, q ≠ 0)	1/2, 3/4, -2/5, 0.75, 0.333…	Pure Numbers, Entire Numbers, Integers	Actual Numbers, Advanced Numbers
Irrational Numbers		Numbers not expressible as p/q (p, q integers, q ≠ 0)	π, e, √2		Actual Numbers, Advanced Numbers
Actual Numbers	ℝ	All rational and irrational numbers	π, e, √2, 1/2, 0, -3	Pure Numbers, Entire Numbers, Integers, Rational Numbers, Irrational Numbers	Advanced Numbers
Advanced Numbers	ℂ	Numbers of the shape a + bi (a, b actual numbers, i² = -1)	2 + 3i, -1 – i, 4	Pure Numbers, Entire Numbers, Integers, Rational Numbers, Actual Numbers, Irrational Numbers
Algebraic Numbers		Roots of polynomial equations with rational coefficients	√2, √3, 1+√5		Actual Numbers, Advanced Numbers
Transcendental Numbers		Numbers that aren’t algebraic	π, e	Irrational Numbers	Actual Numbers, Advanced Numbers

This chart gives a visible illustration of the hierarchical relationship between the assorted quantity techniques. Every set encompasses the properties of its subsets, constructing upon the foundational ideas of counting and measurement to create a wealthy and sophisticated mathematical panorama. Understanding these totally different quantity techniques is prime to greedy the breadth and depth of mathematical ideas and their purposes in numerous fields.

Closure

Thus, we hope this text has offered helpful insights into A Complete Information to Quantity Techniques: Exploring the World of Numbers. We hope you discover this text informative and helpful. See you in our subsequent article!