Decoding The Optimistic Z-Desk: A Complete Information To Understanding And Making use of The Normal Regular Distribution

Decoding the Optimistic Z-Desk: A Complete Information to Understanding and Making use of the Normal Regular Distribution

Associated Articles: Decoding the Optimistic Z-Desk: A Complete Information to Understanding and Making use of the Normal Regular Distribution

Introduction

With enthusiasm, let’s navigate by way of the intriguing matter associated to Decoding the Optimistic Z-Desk: A Complete Information to Understanding and Making use of the Normal Regular Distribution. Let’s weave attention-grabbing info and supply contemporary views to the readers.

Decoding the Optimistic Z-Desk: A Complete Information to Understanding and Making use of the Normal Regular Distribution

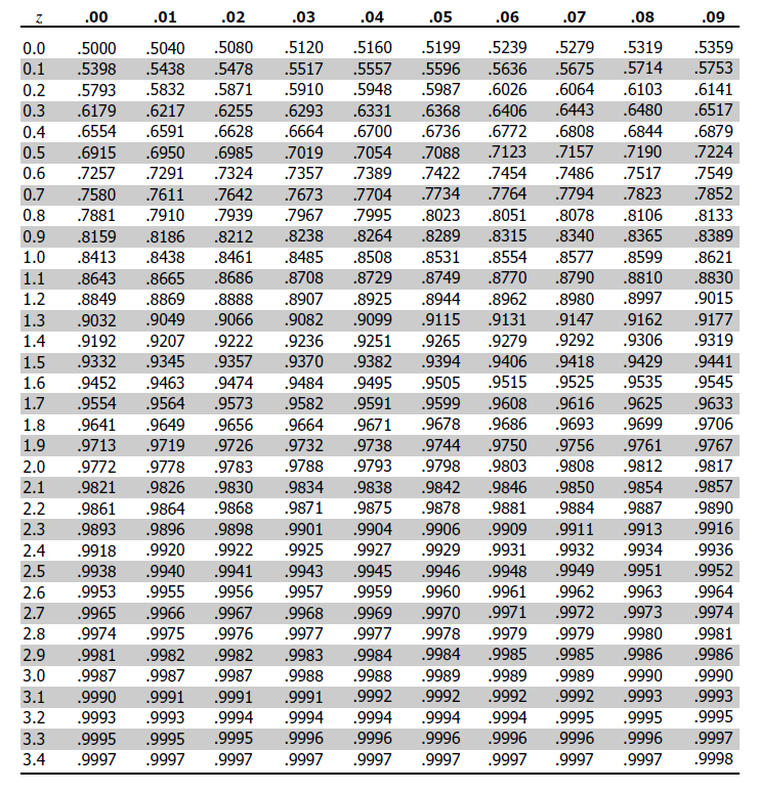
The optimistic z-table, also called the usual regular distribution desk, is an important device in statistics. It gives the cumulative chance related to a given z-score, representing the world below the usual regular curve to the left of that z-score. Understanding and successfully utilizing this desk is key for a variety of statistical analyses, from speculation testing and confidence intervals to chance calculations and course of functionality research. This text delves deep into the optimistic z-table, explaining its development, interpretation, and sensible functions.

The Normal Regular Distribution: A Basis for Understanding

Earlier than we dive into the intricacies of the optimistic z-table, let’s set up a transparent understanding of the usual regular distribution. This distribution is a theoretical chance distribution with a imply (μ) of 0 and a regular deviation (σ) of 1. Its bell-shaped curve is completely symmetrical, with half of the info falling on both aspect of the imply. The full space below the curve is the same as 1, representing 100% of the chance.

The ability of the usual regular distribution lies in its capacity to standardize any regular distribution. This standardization is achieved by way of the z-score transformation:

z = (x – μ) / σ

The place:

• z is the z-score
• x is the person knowledge level
• μ is the inhabitants imply
• σ is the inhabitants commonplace deviation

This transformation converts any usually distributed variable into a regular regular variable with a imply of 0 and a regular deviation of 1. This enables us to make use of the usual regular distribution desk (the z-table) to find out chances related to any usually distributed knowledge, no matter its unique imply and commonplace deviation.

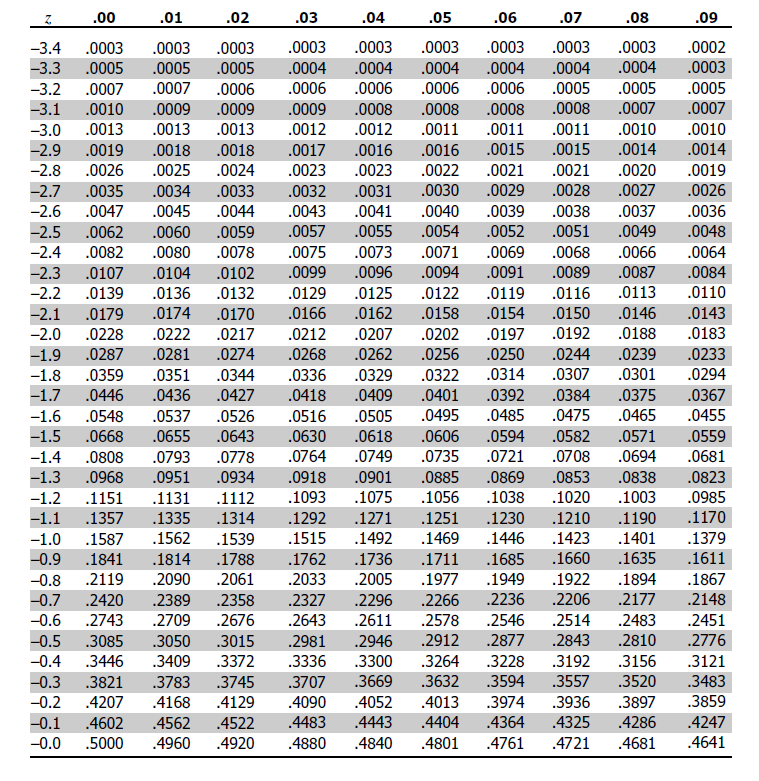
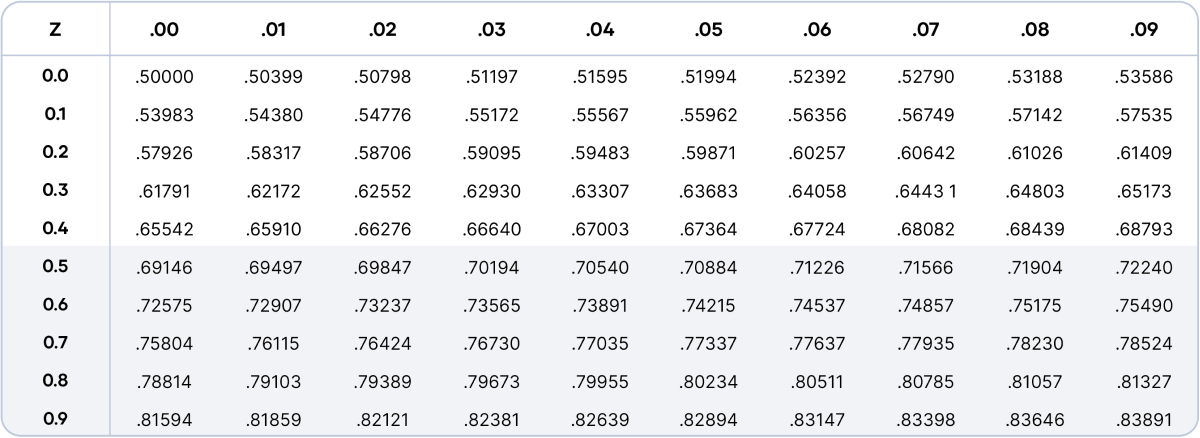
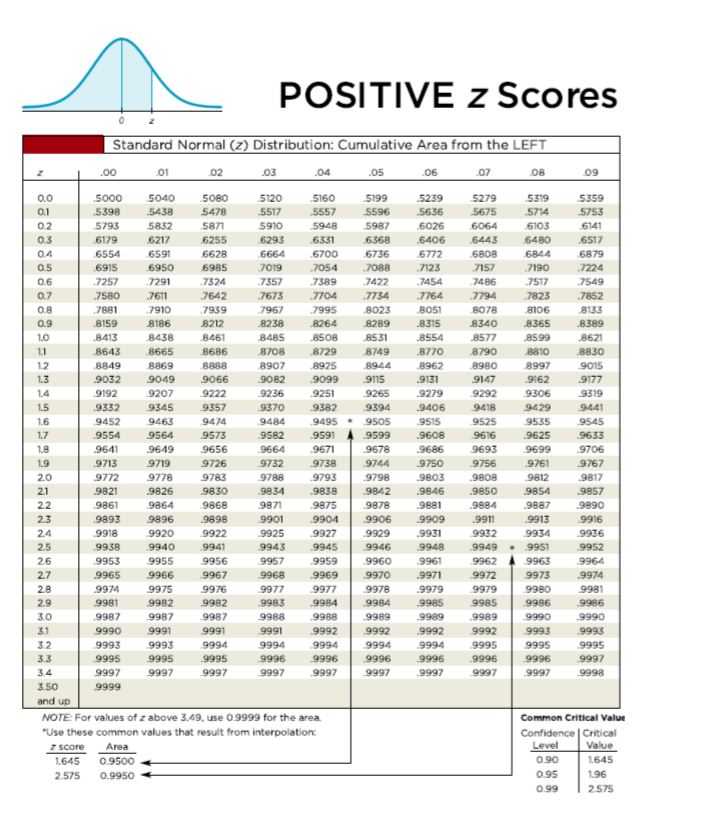
Construction and Interpretation of the Optimistic Z-Desk

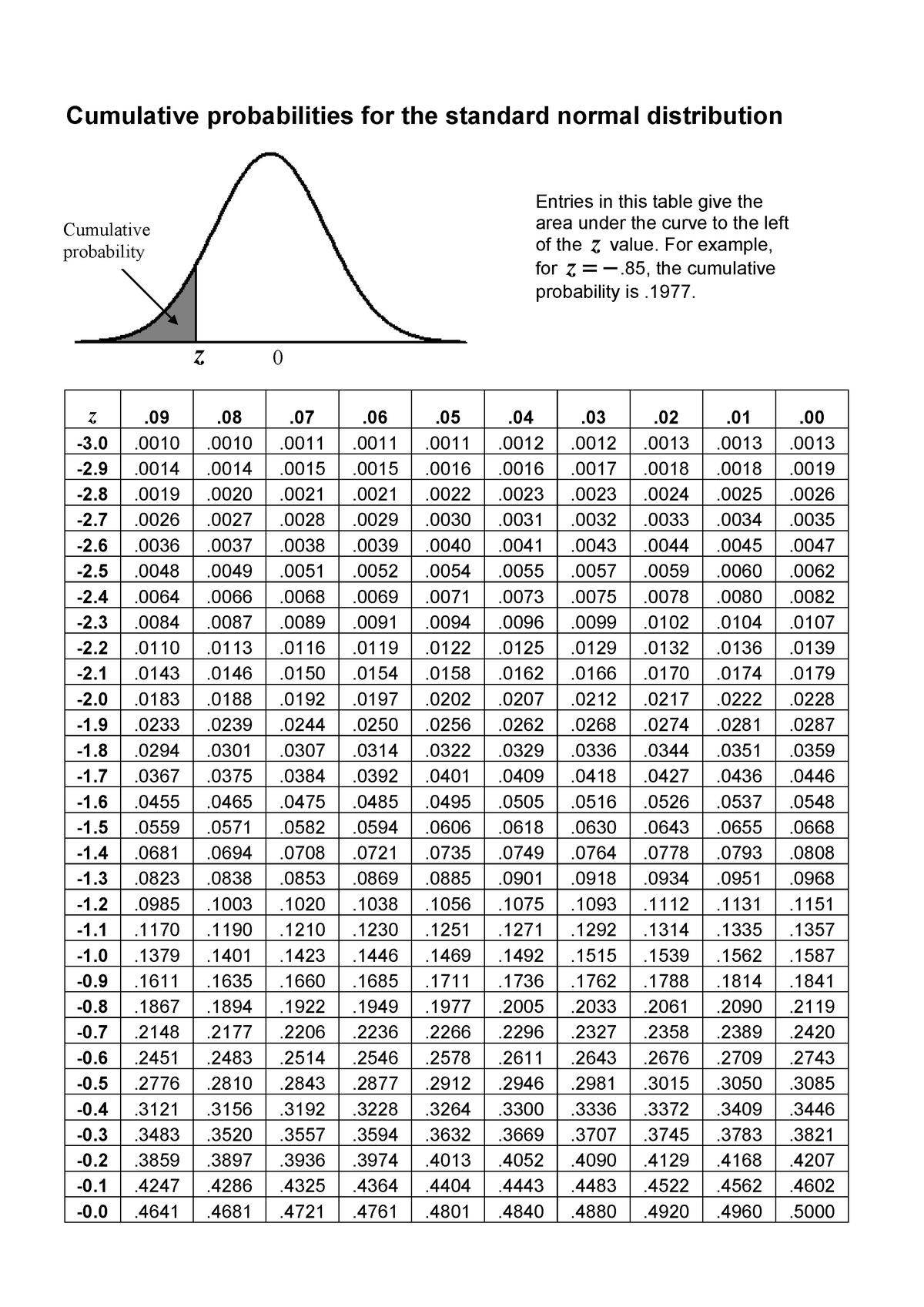
The optimistic z-table is usually a two-dimensional array. The rows signify the integer and tenths place of the z-score, whereas the columns signify the hundredths place. Every cell throughout the desk incorporates a chance worth, representing the world below the usual regular curve to the left of the corresponding z-score.

For instance, to search out the chance related to a z-score of 1.96, you’d find the row akin to 1.9 and the column akin to 0.06. The worth on the intersection of this row and column represents the cumulative chance. This worth signifies the chance {that a} randomly chosen knowledge level from a regular regular distribution can be lower than or equal to 1.96.

Illustrative Instance:

As an instance we wish to discover the chance P(Z ≤ 1.96). We glance up 1.9 within the rows and 0.06 within the columns. The intersection provides us a chance of roughly 0.9750. This implies there is a 97.5% likelihood {that a} randomly chosen knowledge level from a regular regular distribution can be lower than or equal to 1.96.

Functions of the Optimistic Z-Desk

The optimistic z-table’s functions are intensive and span quite a few statistical domains:

• Calculating Possibilities: As demonstrated above, the desk straight gives chances related to particular z-scores. That is essential for figuring out the probability of occasions falling inside sure ranges. As an example, we will calculate the chance of a variable falling between two particular values by discovering the chances for every z-score and subtracting the smaller chance from the bigger one.

• Speculation Testing: In speculation testing, the z-table is significant for figuring out p-values. The p-value represents the chance of observing the obtained outcomes (or extra excessive outcomes) if the null speculation had been true. By evaluating the p-value to the importance stage (alpha), we will determine whether or not to reject or fail to reject the null speculation.

• Confidence Intervals: When setting up confidence intervals, the z-table helps decide the crucial z-score akin to the specified confidence stage. This crucial z-score is then used to calculate the margin of error, which defines the vary inside which the true inhabitants parameter is more likely to lie.

• Course of Functionality Evaluation: In high quality management, the z-table aids in assessing course of functionality. By calculating the z-scores akin to specification limits, we will decide the proportion of output that falls inside acceptable limits. This helps determine potential areas for course of enchancment.

• Regular Approximation to the Binomial Distribution: For giant pattern sizes, the binomial distribution may be approximated by the conventional distribution. The z-table then turns into instrumental in calculating chances related to binomial occasions.

• Understanding percentiles and quantiles: The z-table permits us to find out the worth of a variable akin to a particular percentile or quantile. For instance, discovering the z-score akin to the ninety fifth percentile (0.95 chance) helps decide the worth that separates the highest 5% from the underside 95% of the info.

Limitations and Issues

Whereas the z-table is a strong device, it is important to pay attention to its limitations:

• Assumption of Normality: The z-table is just relevant when the info follows a standard distribution. If the info is considerably non-normal, utilizing the z-table can result in inaccurate outcomes. Checks for normality, such because the Shapiro-Wilk take a look at or the Kolmogorov-Smirnov take a look at, must be performed earlier than making use of the z-table.

• Discrete vs. Steady Information: The z-table is designed for steady knowledge. When coping with discrete knowledge, a continuity correction could also be needed to enhance the accuracy of the approximation.

• Inhabitants vs. Pattern Information: The z-table assumes data of the inhabitants imply and commonplace deviation. If solely pattern knowledge is out there, the t-distribution is likely to be extra acceptable, particularly for smaller pattern sizes.

• Interpolation: The z-table sometimes gives chances for z-scores with two decimal locations. For z-scores with extra decimal locations, interpolation could also be needed, though this will introduce some stage of inaccuracy. Statistical software program packages supply extra exact calculations avoiding the necessity for interpolation.

Conclusion:

The optimistic z-table is an indispensable device for anybody working with statistical knowledge. Its capacity to standardize regular distributions and supply chances related to z-scores makes it invaluable throughout a wide selection of functions. Nevertheless, it is essential to grasp its underlying assumptions and limitations to make sure correct and dependable outcomes. At all times take into account the character of your knowledge and select the suitable statistical technique accordingly. By mastering the usage of the optimistic z-table and understanding its context inside broader statistical ideas, you may considerably improve your capacity to investigate and interpret knowledge successfully. Do not forget that whereas the desk itself is a static useful resource, its utility throughout the dynamic world of statistics requires cautious consideration and significant pondering. Software program packages and on-line calculators can complement the usage of the desk, offering larger precision and effectivity in calculations. Finally, a strong grasp of the z-table empowers you to make knowledgeable selections primarily based on sound statistical reasoning.

Closure

Thus, we hope this text has supplied beneficial insights into Decoding the Optimistic Z-Desk: A Complete Information to Understanding and Making use of the Normal Regular Distribution. We hope you discover this text informative and helpful. See you in our subsequent article!