Decoding The QQ Plot: A Complete Information To Understanding Quantile-Quantile Charts

Decoding the QQ Plot: A Complete Information to Understanding Quantile-Quantile Charts

Associated Articles: Decoding the QQ Plot: A Complete Information to Understanding Quantile-Quantile Charts

Introduction

With enthusiasm, let’s navigate by means of the intriguing matter associated to Decoding the QQ Plot: A Complete Information to Understanding Quantile-Quantile Charts. Let’s weave attention-grabbing data and provide recent views to the readers.

Decoding the QQ Plot: A Complete Information to Understanding Quantile-Quantile Charts

The quantile-quantile plot, or QQ plot, is a robust graphical instrument utilized in statistics to evaluate whether or not a dataset follows a specific theoretical distribution. Not like histograms or density plots that concentrate on the form of the information distribution straight, the QQ plot compares the quantiles of the information to the quantiles of the theoretical distribution. This comparability offers a visible evaluation of the goodness-of-fit, permitting statisticians and information analysts to shortly establish deviations from the assumed distribution and diagnose potential points with their fashions. This text will delve into the intricacies of QQ plots, explaining their development, interpretation, and varied purposes.

Understanding Quantiles

Earlier than diving into QQ plots, it is essential to know the idea of quantiles. A quantile is some extent in a distribution that divides the information into proportions. For instance, the median is the 0.5 quantile (or fiftieth percentile), dividing the information into two equal halves. Different frequent quantiles embody quartiles (dividing the information into 4 components), deciles (ten components), and percentiles (100 components). The quantiles of a dataset are calculated by ordering the information from smallest to largest after which figuring out the values comparable to the specified proportions.

Setting up a QQ Plot

A QQ plot is constructed by plotting the quantiles of the noticed information towards the quantiles of the theoretical distribution being thought of. The method usually includes the next steps:

1. Order the information: Kind the noticed information in ascending order.

2. Calculate the quantiles: Calculate the empirical quantiles of the sorted information. A number of strategies exist for calculating these quantiles, with the most typical being linear interpolation. The selection of technique can barely have an effect on the plot’s look, however the total interpretation stays constant.

3. Calculate theoretical quantiles: Decide the corresponding quantiles from the theoretical distribution. This requires specifying the parameters of the theoretical distribution (e.g., imply and normal deviation for a standard distribution). The theoretical quantiles are sometimes calculated utilizing the inverse cumulative distribution perform (CDF) of the chosen distribution.

4. Plot the factors: Plot the empirical quantiles on the y-axis and the theoretical quantiles on the x-axis. Every level represents a pair of corresponding quantiles.

Decoding a QQ Plot

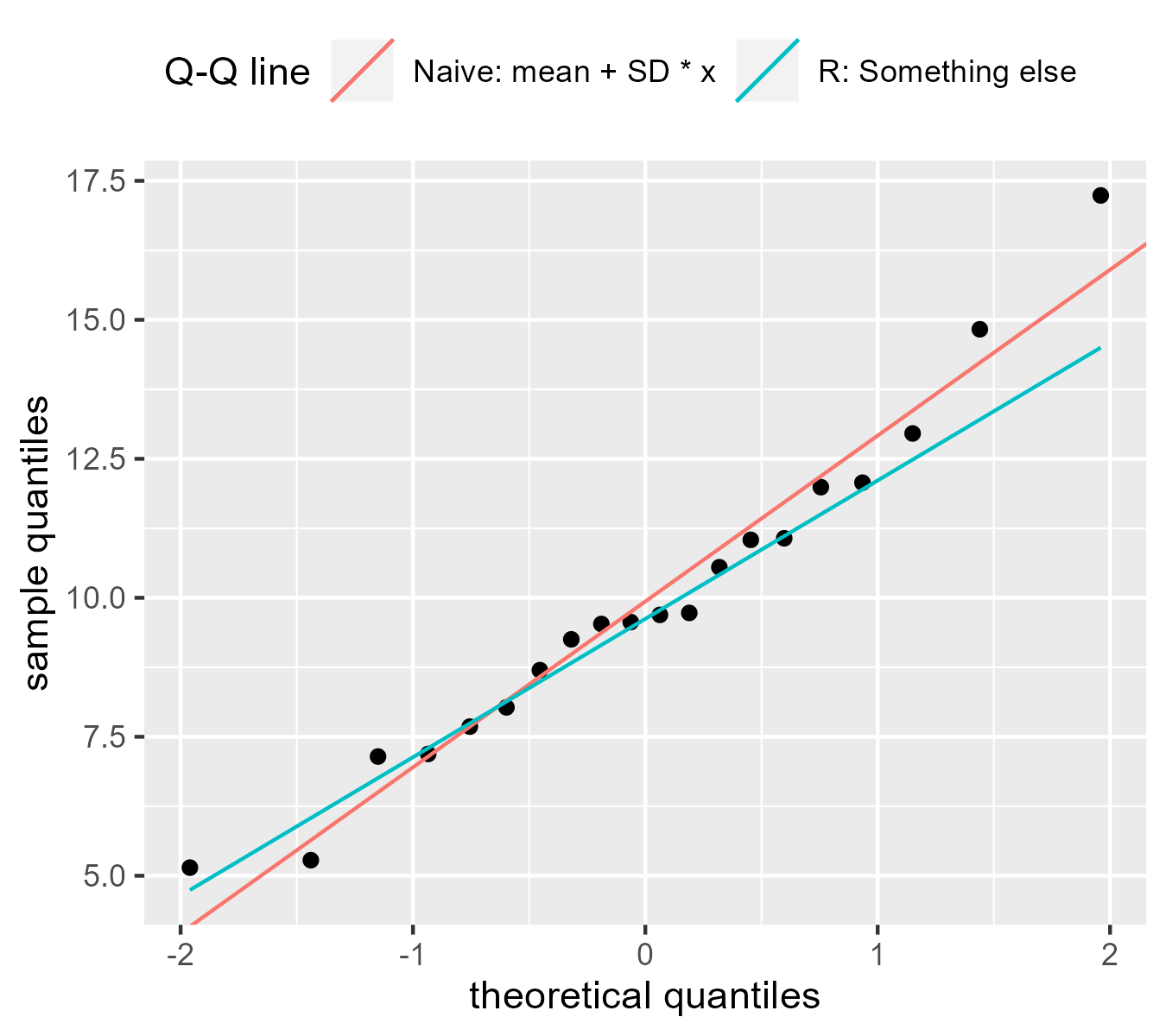
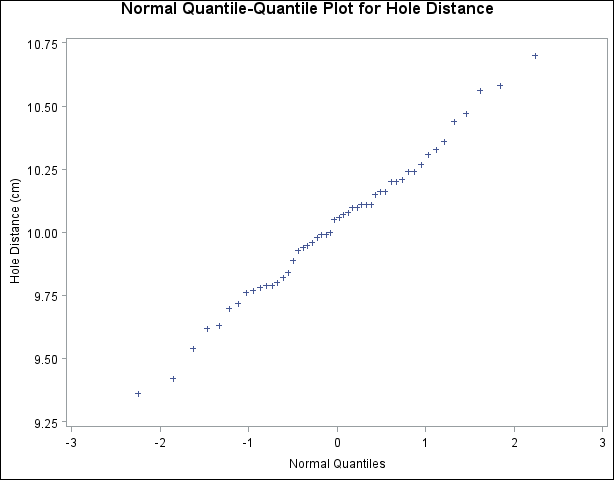
The important thing to decoding a QQ plot lies in understanding how the plotted factors deviate from a straight diagonal line. A wonderfully straight diagonal line signifies an ideal match between the noticed information and the theoretical distribution. Deviations from this line counsel discrepancies between the 2 distributions.

• Linearity: If the factors fall roughly alongside a straight diagonal line, it means that the information follows the theoretical distribution fairly properly. Minor deviations are anticipated, particularly with smaller pattern sizes.

• Systematic Deviations: Systematic deviations from the diagonal line point out particular forms of departures from the theoretical distribution. For instance:

  • Curvature: Curvature means that the tails of the information distribution are heavier or lighter than the theoretical distribution. Upward curvature on the tails implies heavier tails within the information than within the theoretical distribution (e.g., information is likely to be extra liable to outliers). Downward curvature suggests lighter tails.

  • Nonlinearity: Nonlinear patterns point out that the information’s distribution will not be of the assumed sort. The form of the nonlinearity can provide clues in regards to the nature of the deviation.

  • Outliers: Factors that deviate considerably from the general sample can signify outliers within the information. These outliers can considerably affect the interpretation of the plot.

• Non-normality: QQ plots are steadily used to evaluate normality. A QQ plot towards the traditional distribution (typically known as a traditional QQ plot) helps decide if the information is often distributed. Important deviations from a straight line point out non-normality.

Functions of QQ Plots

QQ plots discover widespread purposes throughout varied fields, together with:

• Mannequin Diagnostics: In regression evaluation, QQ plots of the residuals (the variations between noticed and predicted values) can assess whether or not the residuals are usually distributed, an important assumption for a lot of statistical checks. Deviations from normality can point out issues with the mannequin specification or the presence of influential observations.

• Speculation Testing: Whereas not a direct speculation take a look at, QQ plots present a visible assist in assessing the validity of assumptions underlying statistical checks that depend on particular distributional assumptions (e.g., t-tests, ANOVA).

• Information Transformation: If a QQ plot reveals that the information would not comply with the assumed distribution, transformations (e.g., logarithmic, sq. root) may be utilized to the information to enhance the match. The reworked information can then be assessed utilizing a brand new QQ plot.

• Evaluating Distributions: QQ plots can evaluate two datasets straight by plotting the quantiles of 1 dataset towards the quantiles of the opposite. This enables for a visible comparability of the shapes of the 2 distributions, revealing similarities and variations.

• Excessive Worth Concept: QQ plots are essential in excessive worth idea, the place the main focus is on the tail conduct of distributions. They assist establish the suitable excessive worth distribution for modeling excessive occasions.

Limitations of QQ Plots

Whereas QQ plots are invaluable instruments, they’ve limitations:

• Subjectivity: Decoding QQ plots may be considerably subjective, significantly when coping with small pattern sizes or refined deviations from the theoretical distribution. Formal statistical checks of goodness-of-fit is likely to be mandatory for extra goal assessments.

• Sensitivity to Outliers: Outliers can closely affect the looks of a QQ plot, making it tough to evaluate the general distribution precisely. Strong strategies for estimating quantiles can mitigate this situation.

• Not a Substitute for Formal Exams: QQ plots ought to be used as a complementary instrument alongside formal goodness-of-fit checks (e.g., Kolmogorov-Smirnov take a look at, Shapiro-Wilk take a look at). They supply a visible understanding of the information’s distribution however do not provide a definitive statistical measure of goodness-of-fit.

Conclusion

The QQ plot is a flexible and insightful graphical instrument for assessing the match of knowledge to a theoretical distribution. Its skill to visually spotlight deviations from the assumed distribution makes it an indispensable instrument for information analysts and statisticians. By understanding the rules behind its development and interpretation, practitioners can leverage its energy to diagnose potential issues of their fashions, enhance information evaluation, and make extra knowledgeable choices. Nonetheless, it is important to do not forget that QQ plots ought to be used along with different statistical strategies for a complete and sturdy evaluation. The mixture of visible inspection and formal statistical checks offers probably the most full image of the information’s distribution and its conformity to the theoretical mannequin.

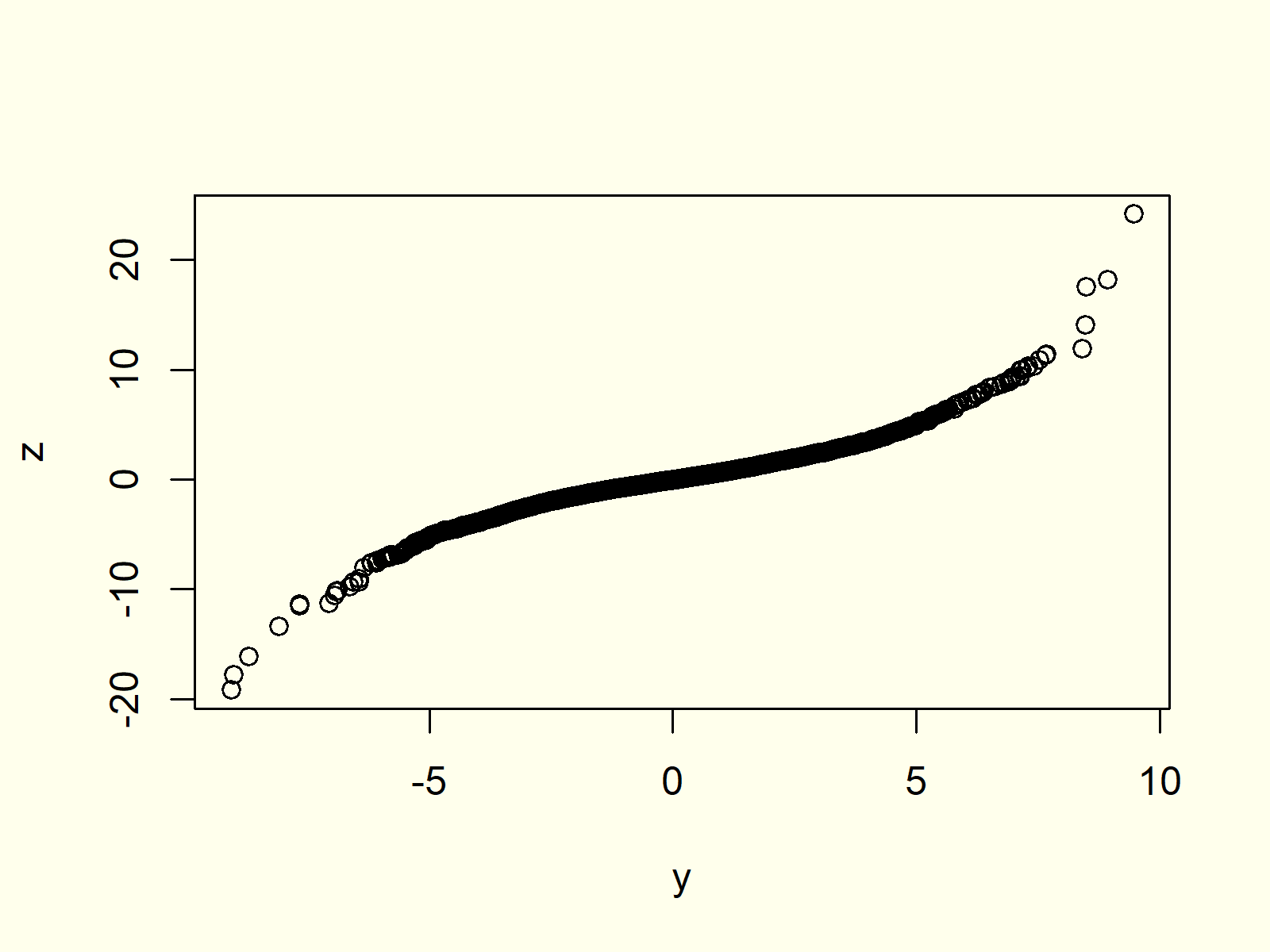
Closure

Thus, we hope this text has supplied worthwhile insights into Decoding the QQ Plot: A Complete Information to Understanding Quantile-Quantile Charts. We hope you discover this text informative and helpful. See you in our subsequent article!