Mastering Quadrilaterals: A Complete Information To Space Calculation With Anchor Chart Examples

Mastering Quadrilaterals: A Complete Information to Space Calculation with Anchor Chart Examples

Associated Articles: Mastering Quadrilaterals: A Complete Information to Space Calculation with Anchor Chart Examples

Introduction

With nice pleasure, we are going to discover the intriguing matter associated to Mastering Quadrilaterals: A Complete Information to Space Calculation with Anchor Chart Examples. Let’s weave attention-grabbing data and provide recent views to the readers.

Mastering Quadrilaterals: A Complete Information to Space Calculation with Anchor Chart Examples

Quadrilaterals, four-sided polygons, type a elementary constructing block in geometry. Understanding their properties, significantly how you can calculate their space, is essential for achievement in arithmetic and associated fields. This text offers a complete information to calculating the world of assorted quadrilaterals, complemented by detailed anchor chart examples to help visualization and memorization. We’ll transfer from the only to extra advanced shapes, highlighting the formulation and their functions.

I. Understanding the Anchor Chart Strategy

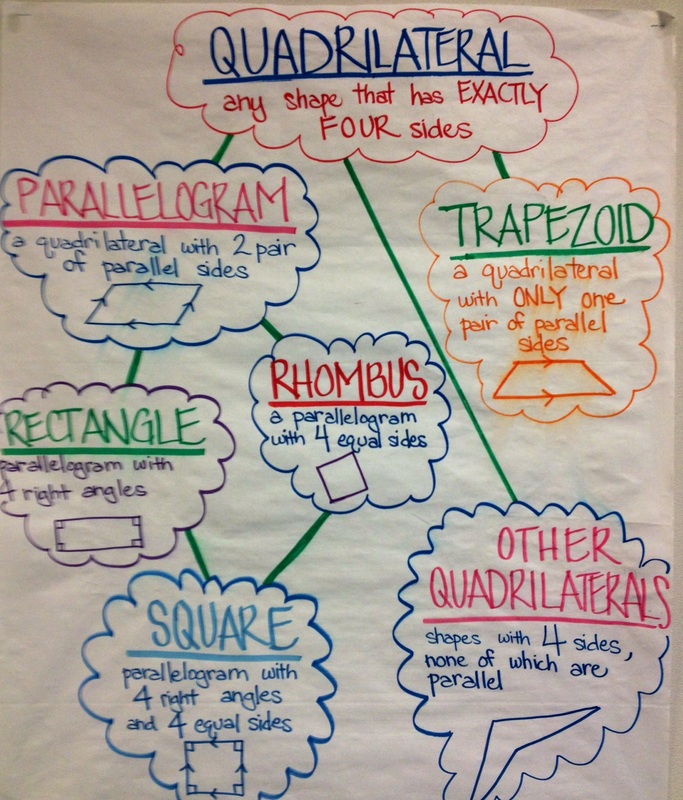
An anchor chart is a visible assist designed to offer a fast reference and abstract of key ideas. For space calculations of quadrilaterals, an efficient anchor chart ought to embrace:

• Sort of Quadrilateral: Clearly labeled with diagrams of every quadrilateral sort (sq., rectangle, parallelogram, rhombus, trapezoid, kite).
• Space Components: The particular formulation for calculating the world of every quadrilateral, written concisely and clearly.
• Variable Definitions: A short clarification of what every variable within the formulation represents (e.g., base, top, diagonal).
• Diagram with Labeled Variables: A labeled diagram displaying the related measurements wanted for the formulation.
• Instance Calculation: A worked-out instance demonstrating the applying of the formulation with numerical values.

II. The Basic Quadrilaterals: Squares and Rectangles

These are the only quadrilaterals to grasp and calculate the world for.

A. Sq.:

• Definition: A quadrilateral with 4 equal sides and 4 proper angles.
• Space Components: Space = aspect * aspect = s²
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Sq.	Space = s²	s = size of a aspect	[Diagram of a square with side ‘s’ labeled]	If s = 5 cm, Space = 5² = 25 cm²

B. Rectangle:

• Definition: A quadrilateral with 4 proper angles and reverse sides equal in size.
• Space Components: Space = size width = l w
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Rectangle	Space = l * w	l = size, w = width	[Diagram of a rectangle with length ‘l’ and width ‘w’ labeled]	If l = 8 cm and w = 4 cm, Space = 8 * 4 = 32 cm²

III. Parallelograms and Rhombuses: Introducing Peak

Parallelograms and rhombuses introduce the idea of "top" which is essential for space calculation. The peak is the perpendicular distance between two parallel sides.

A. Parallelogram:

• Definition: A quadrilateral with reverse sides parallel and equal in size.
• Space Components: Space = base top = b h
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Parallelogram	Space = b * h	b = base, h = top (perpendicular distance between bases)	[Diagram of a parallelogram with base ‘b’ and height ‘h’ labeled. Height is shown as a perpendicular line]	If b = 10 cm and h = 6 cm, Space = 10 * 6 = 60 cm²

B. Rhombus:

• Definition: A quadrilateral with all 4 sides equal in size.
• Space Components: Space = base top = b h (or Space = ½ d₁ d₂, the place d₁ and d₂ are the lengths of the diagonals)
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Rhombus	Space = b h (or ½ d₁ * d₂)	b = base, h = top, d₁ & d₂ = diagonals	[Diagram of a rhombus with base ‘b’, height ‘h’, and diagonals d₁ and d₂ labeled]	If b = 7 cm and h = 5 cm, Space = 7 5 = 35 cm². If d₁ = 8 cm and d₂ = 6 cm, Space = ½ 8 * 6 = 24 cm²

IV. Trapezoids: Averaging the Bases

Trapezoids require a barely extra advanced formulation as a result of their unequal parallel sides.

A. Trapezoid:

• Definition: A quadrilateral with one pair of parallel sides (bases).
• Space Components: Space = ½ (base₁ + base₂) top = ½(b₁ + b₂)h
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Trapezoid	Space = ½(b₁ + b₂)h	b₁ & b₂ = parallel bases, h = top (perpendicular distance between bases)	[Diagram of a trapezoid with bases b₁ and b₂ and height ‘h’ labeled. Height is shown as a perpendicular line]	If b₁ = 4 cm, b₂ = 8 cm, and h = 5 cm, Space = ½(4 + 8) * 5 = 30 cm²

V. Kites: Using Diagonals

Kites, like rhombuses, may be conveniently calculated utilizing their diagonals.

A. Kite:

• Definition: A quadrilateral with two pairs of adjoining sides equal in size.
• Space Components: Space = ½ diagonal₁ diagonal₂ = ½d₁d₂
• Anchor Chart Entry:

Sort of Quadrilateral	Space Components	Variable Definitions	Diagram	Instance
Kite	Space = ½d₁d₂	d₁ & d₂ = diagonals	[Diagram of a kite with diagonals d₁ and d₂ labeled]	If d₁ = 12 cm and d₂ = 8 cm, Space = ½ 12 8 = 48 cm²

VI. Superior Issues and Functions

• Models: All the time keep in mind to incorporate acceptable items (cm², m², and so forth.) in your space calculations.
• Irregular Quadrilaterals: For quadrilaterals that do not match into the above classes, you would possibly must divide them into smaller triangles or rectangles to calculate the world.
• Actual-world functions: Understanding quadrilateral space is significant in lots of fields, together with:
  • Building: Calculating ground house, roof areas, land plots.
  • Engineering: Designing buildings, calculating floor areas.
  • Cartography: Figuring out land areas on maps.
  • Artwork and Design: Creating symmetrical patterns and shapes.

VII. Increasing the Anchor Chart: Incorporating Irregular Quadrilaterals

The anchor chart may be expanded to incorporate strategies for calculating the world of irregular quadrilaterals. This would possibly contain:

• Triangulation: Dividing the quadrilateral into two triangles utilizing a diagonal as a typical aspect. Calculate the world of every triangle utilizing the formulation ½ base top after which add the areas collectively.
• Coordinate Geometry: If the vertices of the quadrilateral are given as coordinates, the world may be calculated utilizing the determinant technique or different vector methods. This strategy is extra superior and requires a stronger understanding of coordinate geometry.

VIII. Conclusion:

This text offers a radical information to calculating the world of assorted quadrilaterals, emphasizing the usage of anchor charts as a robust studying instrument. By making a visually interesting and informative anchor chart, college students can rapidly entry and apply the required formulation for various quadrilateral sorts. Remembering the formulation and understanding the underlying ideas will considerably enhance problem-solving abilities in geometry and associated fields. The inclusion of labored examples and real-world functions reinforces the sensible relevance of those ideas, making studying extra participating and significant. Bear in mind to adapt and increase your anchor chart as you study extra advanced geometrical ideas. The extra visible and arranged your assets are, the extra successfully you’ll grasp the topic.

Closure

Thus, we hope this text has supplied invaluable insights into Mastering Quadrilaterals: A Complete Information to Space Calculation with Anchor Chart Examples. We hope you discover this text informative and helpful. See you in our subsequent article!