Mastering The Z-Desk In Excel: A Complete Information To Regular Distribution Evaluation

Mastering the Z-Desk in Excel: A Complete Information to Regular Distribution Evaluation

Associated Articles: Mastering the Z-Desk in Excel: A Complete Information to Regular Distribution Evaluation

Introduction

With nice pleasure, we’ll discover the intriguing matter associated to Mastering the Z-Desk in Excel: A Complete Information to Regular Distribution Evaluation. Let’s weave fascinating info and supply contemporary views to the readers.

Mastering the Z-Desk in Excel: A Complete Information to Regular Distribution Evaluation

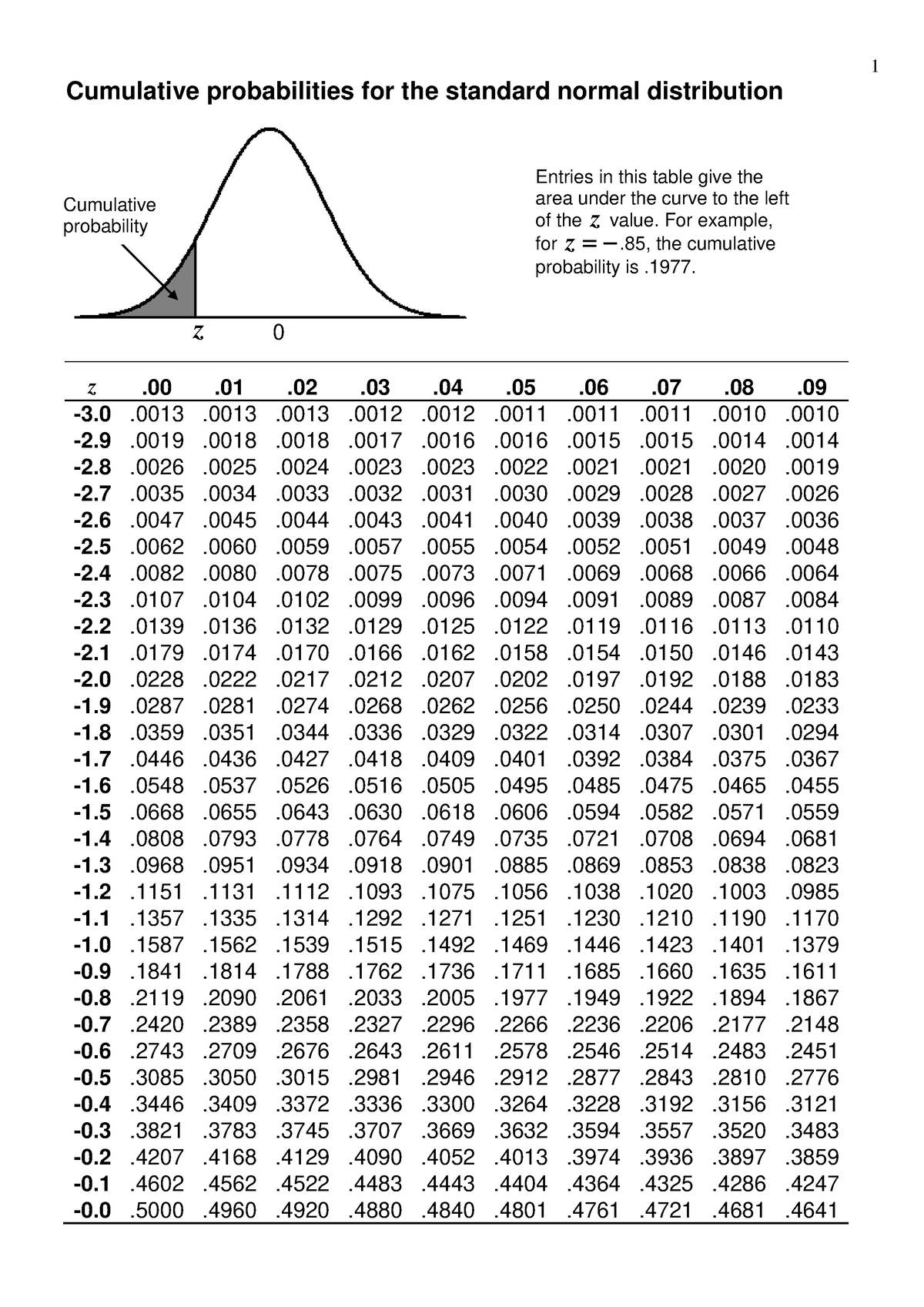
The conventional distribution, typically depicted as a bell curve, is a basic idea in statistics. It describes the chance distribution of many naturally occurring phenomena, from human heights and weights to check scores and monetary market fluctuations. Understanding and using the conventional distribution is essential for varied analytical duties, and a key device on this course of is the Z-table (also referred to as the usual regular distribution desk). Whereas yow will discover Z-tables in statistical textbooks, Excel provides a strong and environment friendly different for working with this very important device, eliminating the necessity for handbook desk lookup and considerably accelerating your evaluation. This text gives a complete information to understanding and utilizing the Z-table throughout the Excel surroundings.

Understanding the Z-Rating and the Customary Regular Distribution

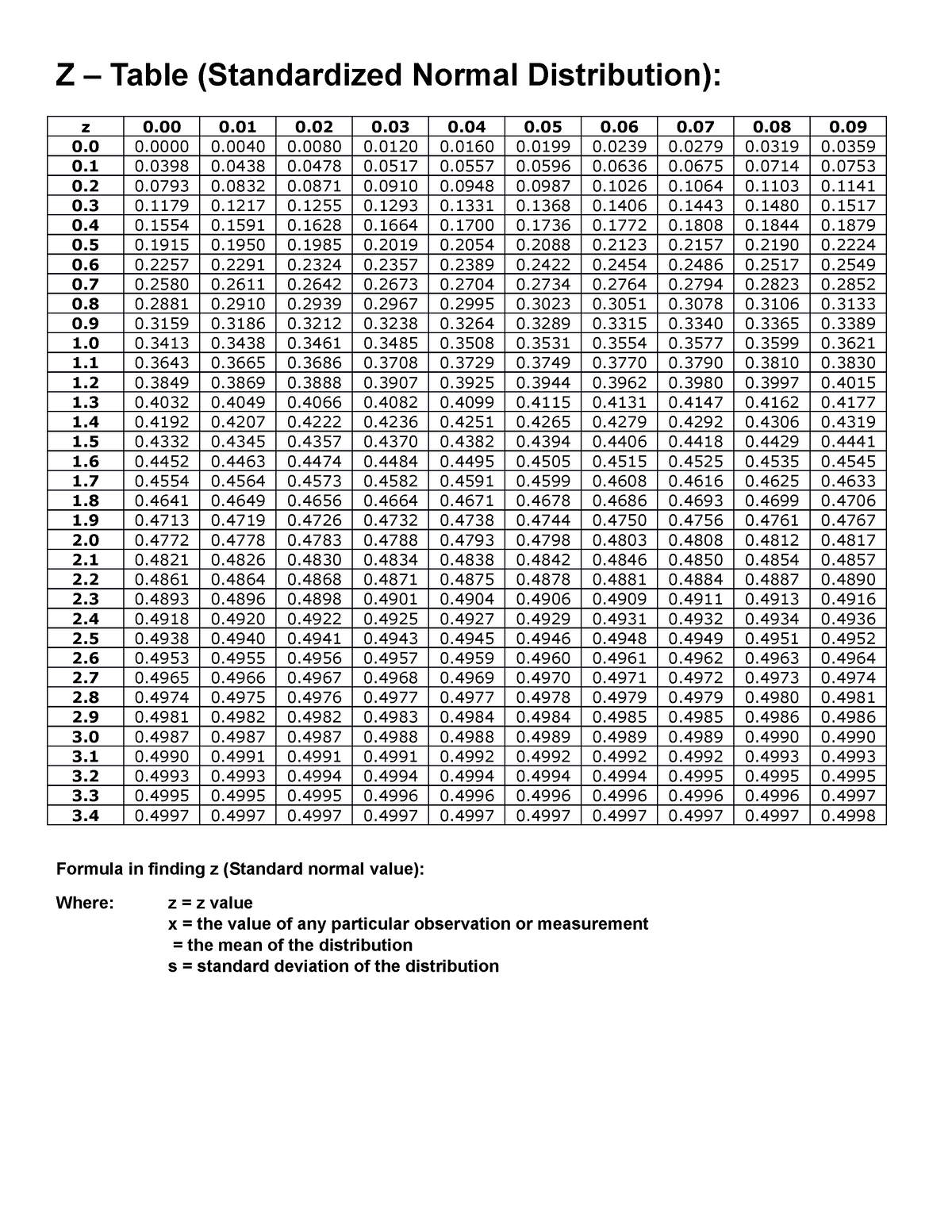
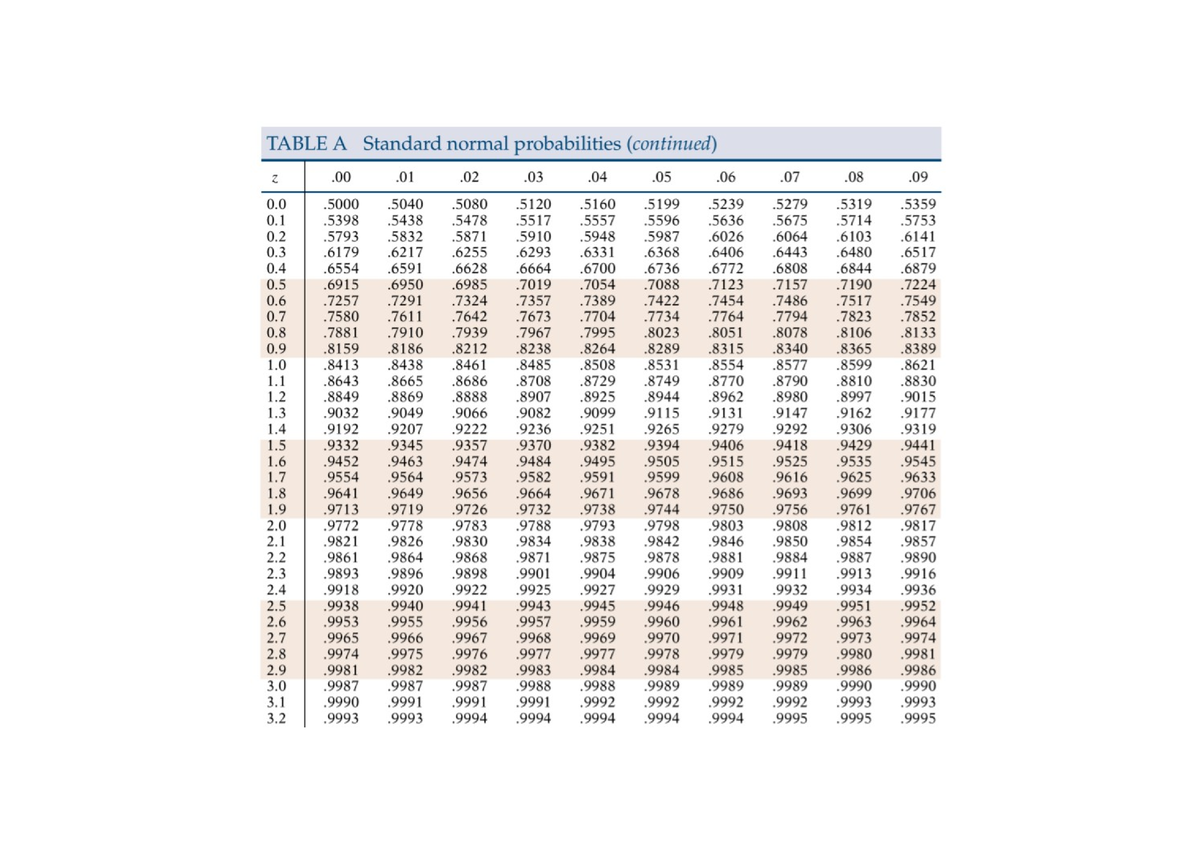
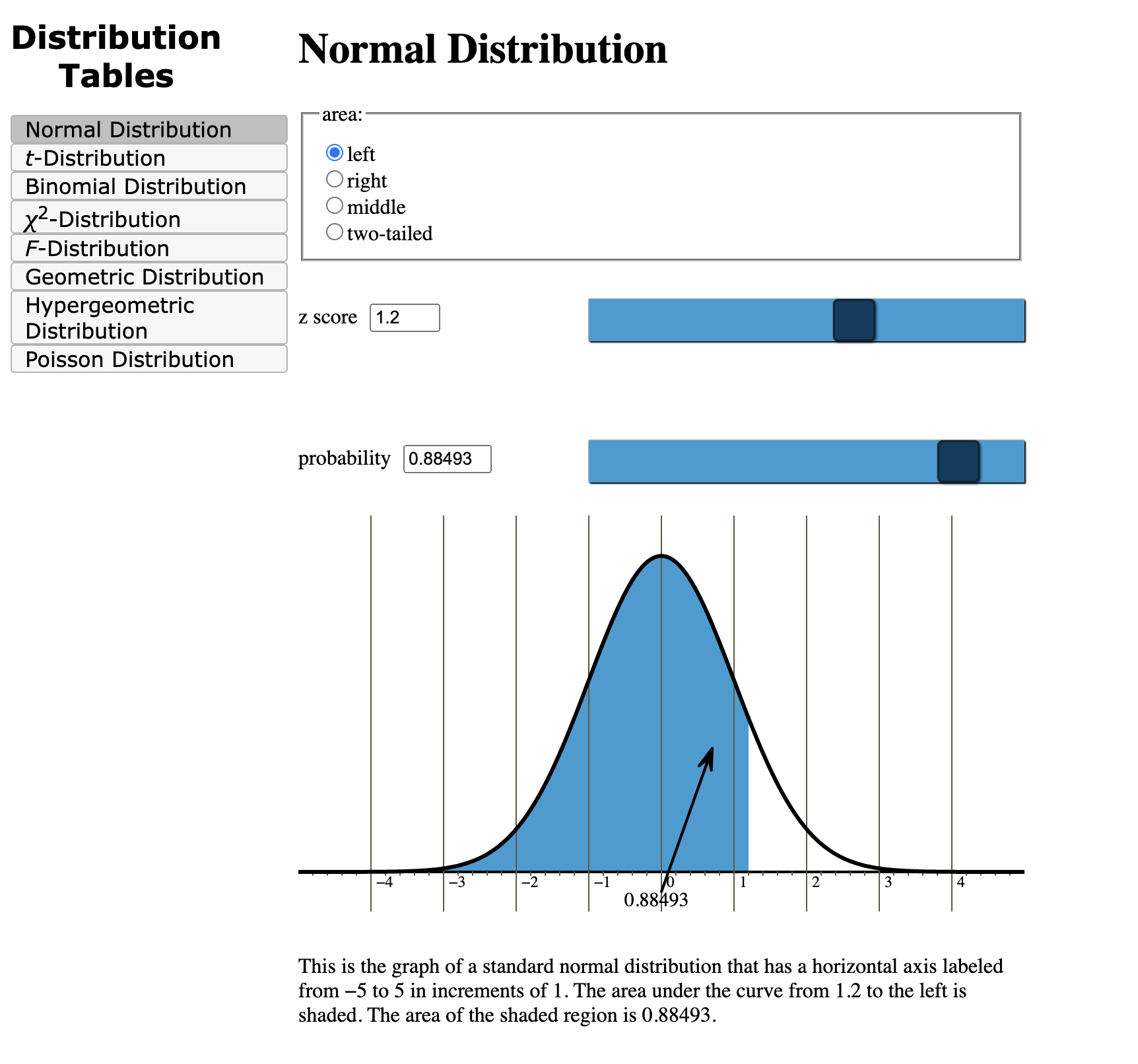
Earlier than delving into Excel’s capabilities, it is important to know the core ideas of Z-scores and the usual regular distribution. The Z-score, also referred to as the standardized rating, represents the variety of commonplace deviations a knowledge level lies from the imply of a standard distribution. A optimistic Z-score signifies the information level is above the imply, whereas a damaging Z-score signifies it is beneath the imply. A Z-score of 0 signifies the information level is strictly on the imply.

The usual regular distribution is a particular case of the conventional distribution with a imply (μ) of 0 and a regular deviation (σ) of 1. This standardization permits for simple comparability of knowledge from totally different regular distributions. The Z-table gives the cumulative chance related to a given Z-score in the usual regular distribution. In different phrases, it tells you the chance of observing a price lower than or equal to a selected Z-score.

Utilizing Excel Features for Z-Desk Calculations

Excel provides a number of built-in capabilities that successfully change the necessity for a bodily Z-table. These capabilities enable for exact and speedy calculations, eliminating the potential for human error related to handbook desk lookups. The first capabilities used for Z-table evaluation in Excel are:

• NORM.S.DIST(z, cumulative): This perform calculates the cumulative commonplace regular distribution perform. The ‘z’ argument represents the Z-score, and the ‘cumulative’ argument is a logical worth (TRUE or FALSE). Setting ‘cumulative’ to TRUE (the default) returns the cumulative chance (space underneath the curve to the left of the Z-score). Setting it to FALSE returns the chance density perform (the peak of the curve on the Z-score).

• NORM.S.INV(chance): This perform is the inverse of NORM.S.DIST. It takes a chance (between 0 and 1) as enter and returns the corresponding Z-score. That is significantly helpful when you realize the chance and want to seek out the related Z-score.

• NORM.DIST(x, imply, standard_dev, cumulative): This perform is a extra normal model of NORM.S.DIST, permitting you to work with regular distributions which have means and commonplace deviations apart from 0 and 1, respectively. The ‘x’ argument is the information level, ‘imply’ is the inhabitants imply, ‘standard_dev’ is the inhabitants commonplace deviation, and ‘cumulative’ works the identical as in NORM.S.DIST.

Sensible Purposes and Examples

Let’s illustrate the usage of these capabilities with some sensible examples:

Instance 1: Discovering the Cumulative Likelihood

Suppose you wish to discover the chance {that a} randomly chosen information level from a regular regular distribution is lower than or equal to 1.5. Utilizing Excel, you’d enter the next formulation:

=NORM.S.DIST(1.5,TRUE)

This can return a price of roughly 0.9332, indicating that there is a 93.32% probability of observing a price lower than or equal to 1.5 in a regular regular distribution.

Instance 2: Discovering the Likelihood between Two Z-scores

To search out the chance {that a} information level falls between two Z-scores, say -1 and 1, you’d calculate the cumulative chance for every Z-score and discover the distinction:

=NORM.S.DIST(1,TRUE) - NORM.S.DIST(-1,TRUE)

This can return a price of roughly 0.6827, representing the chance {that a} information level lies inside one commonplace deviation of the imply (roughly 68%).

Instance 3: Discovering the Z-score for a Given Likelihood

If you realize the chance and wish to discover the corresponding Z-score, use the NORM.S.INV perform. As an illustration, to seek out the Z-score that corresponds to a cumulative chance of 0.95, you’d use:

=NORM.S.INV(0.95)

This can return a Z-score of roughly 1.645.

Instance 4: Working with Non-Customary Regular Distributions

Think about a dataset with a imply of fifty and a regular deviation of 10. To search out the chance {that a} randomly chosen information level is lower than 60, you’d use the NORM.DIST perform:

=NORM.DIST(60,50,10,TRUE)

This can return the cumulative chance for a price of 60 on this particular regular distribution.

Superior Purposes and Concerns

The Z-table and its Excel equivalents have quite a few purposes past primary chance calculations. They’re integral to:

• Speculation testing: Figuring out the importance of statistical outcomes.
• Confidence intervals: Estimating the vary inside which a inhabitants parameter seemingly lies.
• High quality management: Monitoring course of variability and detecting outliers.
• Danger administration: Assessing the chance of maximum occasions.

Limitations and Alternate options

Whereas Excel’s capabilities are extremely environment friendly, it is vital to pay attention to potential limitations:

• Accuracy: Whereas Excel gives excessive precision, rounding errors can happen in complicated calculations.
• Assumptions: The accuracy of Z-table calculations depends on the idea of normality. In case your information considerably deviates from a standard distribution, different statistical strategies could be extra acceptable. Think about using different distributions (e.g., t-distribution for small pattern sizes) or non-parametric strategies.

Conclusion

The Z-table, carried out effectively by means of Excel’s capabilities, is an indispensable device for anybody working with regular distributions. Understanding its utility and mastering the related Excel capabilities considerably enhances the velocity and accuracy of statistical evaluation. By combining a powerful theoretical understanding of the conventional distribution with the sensible capabilities of Excel, you’ll be able to confidently deal with a variety of statistical issues and extract beneficial insights out of your information. Bear in mind to all the time critically assess the assumptions underlying your evaluation and think about different strategies when needed to make sure the validity and reliability of your outcomes. This information serves as a foundational understanding, and additional exploration of statistical ideas and Excel’s superior options will improve your analytical prowess even additional.

Closure

Thus, we hope this text has offered beneficial insights into Mastering the Z-Desk in Excel: A Complete Information to Regular Distribution Evaluation. We hope you discover this text informative and useful. See you in our subsequent article!