Navigating The Regular Distribution: A Complete Information To The Z-Chart

Navigating the Regular Distribution: A Complete Information to the Z-Chart

Associated Articles: Navigating the Regular Distribution: A Complete Information to the Z-Chart

Introduction

With enthusiasm, let’s navigate via the intriguing subject associated to Navigating the Regular Distribution: A Complete Information to the Z-Chart. Let’s weave attention-grabbing data and provide recent views to the readers.

Navigating the Regular Distribution: A Complete Information to the Z-Chart

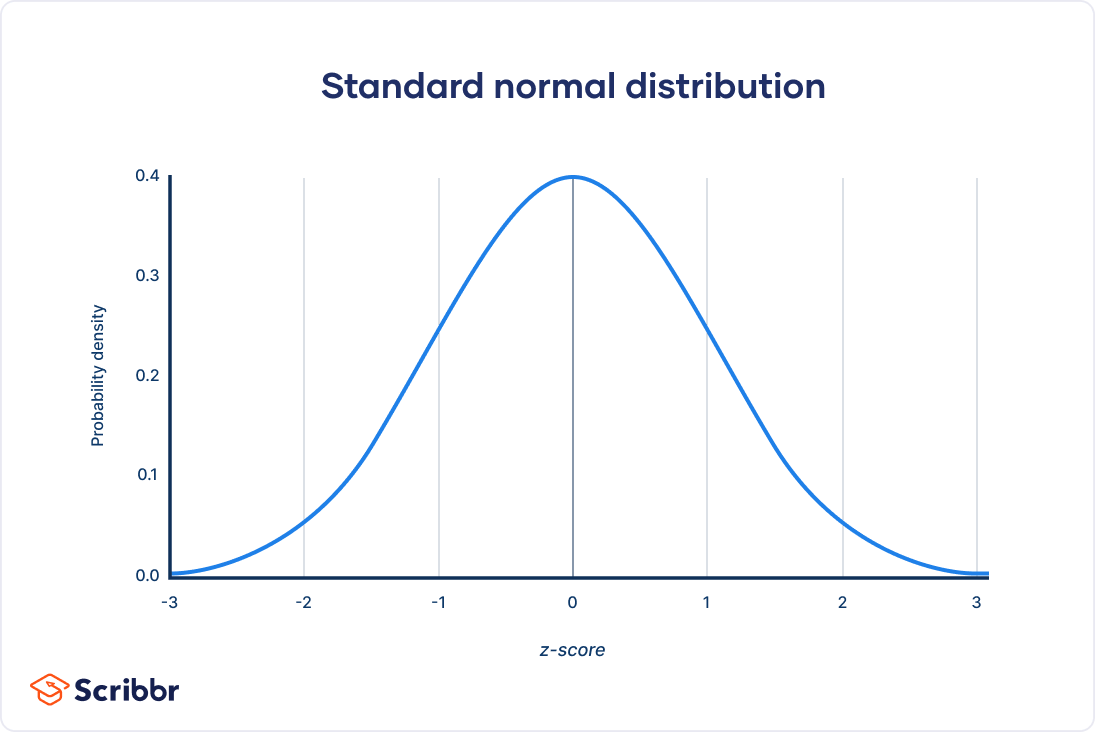
The conventional distribution, typically depicted as a bell curve, is a basic idea in statistics. It describes the chance distribution of a steady random variable, characterised by its symmetry and focus round a central imply. Understanding the traditional distribution is essential throughout quite a few fields, from finance and engineering to drugs and social sciences. A key instrument for working with the traditional distribution is the Z-chart, also referred to as the usual regular distribution desk. This text supplies a complete overview of the Z-chart and its functions.

Understanding the Regular Distribution

Earlier than delving into the Z-chart, it is important to understand the core properties of the traditional distribution:

• Symmetry: The distribution is completely symmetrical round its imply (μ). Which means the chance of observing a price under the imply is the same as the chance of observing a price above the imply.

• Imply, Median, and Mode: In a standard distribution, the imply, median, and mode are all equal. This central tendency simplifies calculations and interpretations.

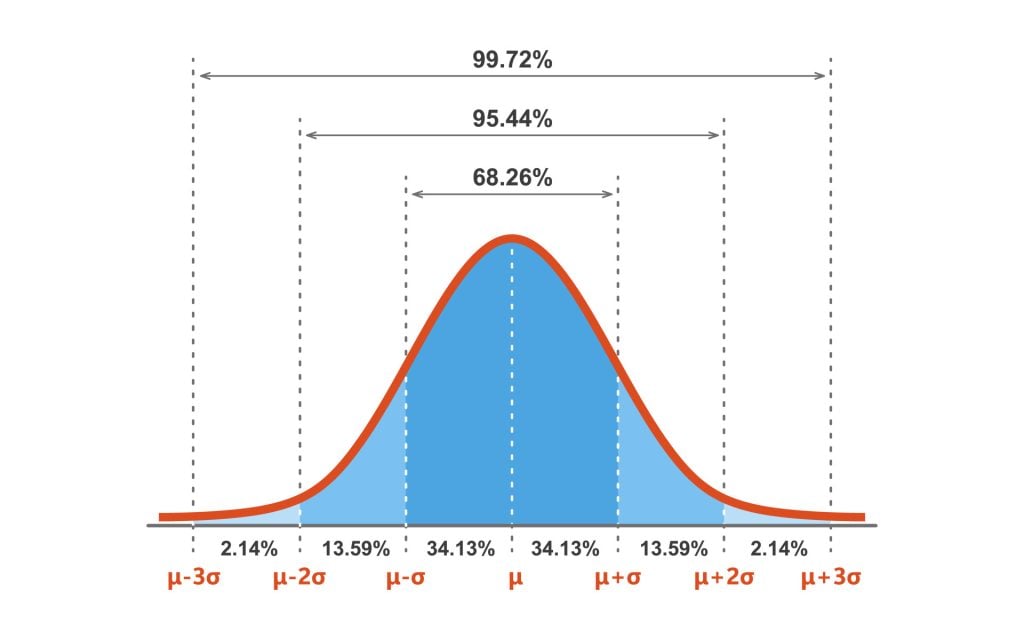
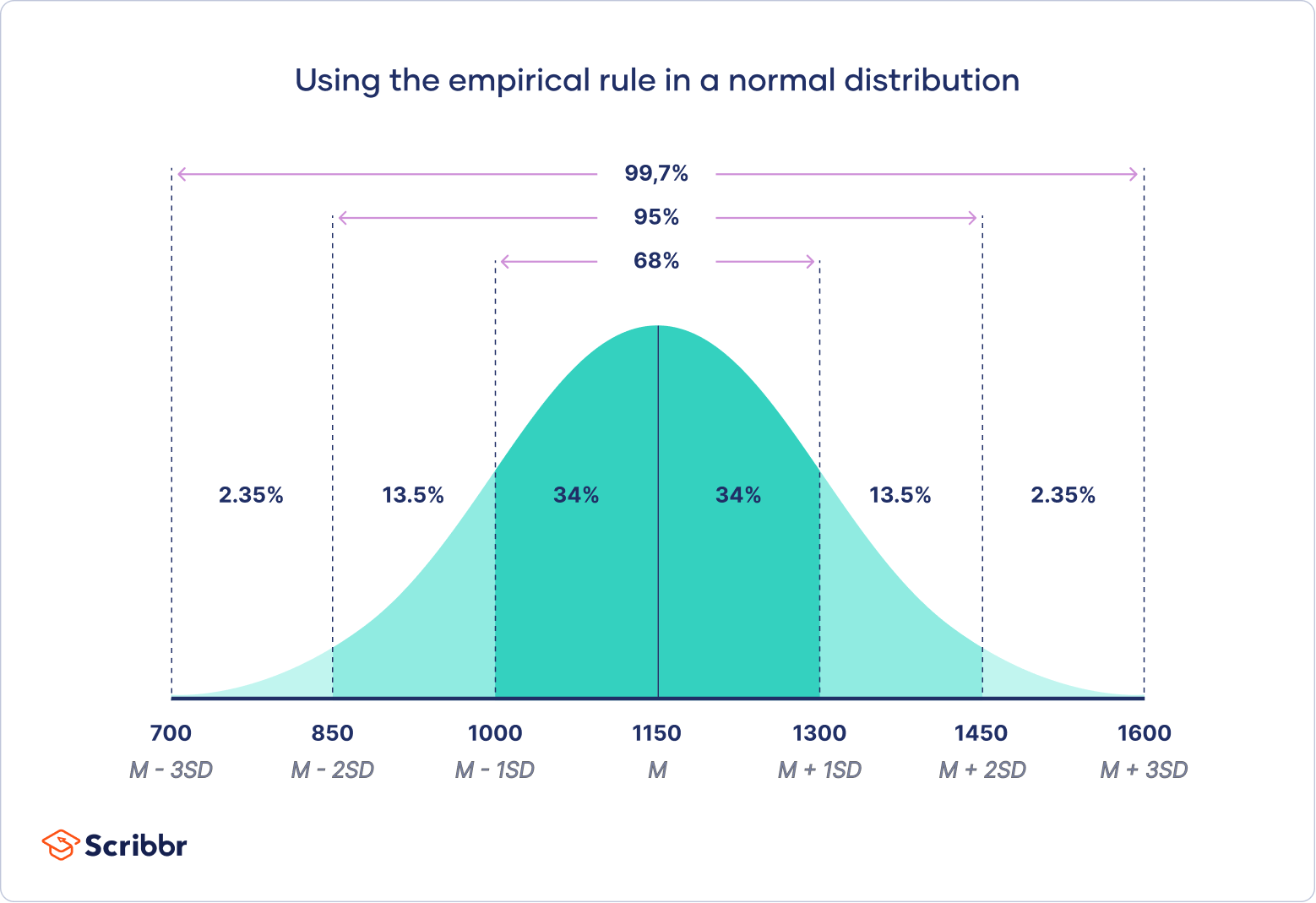
• Normal Deviation (σ): The usual deviation determines the unfold or dispersion of the info. A smaller commonplace deviation signifies a narrower, extra concentrated distribution, whereas a bigger commonplace deviation signifies a wider, extra spread-out distribution. 68% of the info falls inside one commonplace deviation of the imply, 95% inside two commonplace deviations, and 99.7% inside three commonplace deviations (the empirical rule or 68-95-99.7 rule).

• Steady Variable: The conventional distribution describes steady variables, that means the variable can tackle any worth inside a given vary. Peak, weight, and temperature are examples of variables that always observe a standard distribution.

The Significance of Standardization: Introducing the Z-score

Whereas the traditional distribution is conceptually highly effective, working instantly with completely different means and commonplace deviations throughout numerous datasets will be cumbersome. That is the place standardization is available in. Standardization transforms any regular distribution into a typical regular distribution, which has a imply of 0 and a typical deviation of 1. This transformation is achieved utilizing the Z-score:

Z = (X – μ) / σ

The place:

• Z is the Z-score
• X is the person information level
• μ is the inhabitants imply
• σ is the inhabitants commonplace deviation

The Z-score represents the variety of commonplace deviations a knowledge level is away from the imply. A optimistic Z-score signifies the info level is above the imply, whereas a adverse Z-score signifies it is under the imply. For instance, a Z-score of 1.5 means the info level is 1.5 commonplace deviations above the imply.

The Z-Chart: A Desk of Chances

The Z-chart (commonplace regular distribution desk) is a vital instrument for figuring out possibilities related to Z-scores. It supplies the cumulative chance (space below the curve) to the left of a given Z-score. This implies it tells you the chance of observing a price lower than or equal to a particular Z-score.

The Z-chart is often organized into two components:

• Constructive Z-scores: This part lists possibilities for optimistic Z-scores.
• Unfavourable Z-scores: This part lists possibilities for adverse Z-scores. As a result of symmetry of the traditional distribution, the chance for a adverse Z-score is solely 1 minus the chance for the corresponding optimistic Z-score.

Utilizing the Z-Chart: A Step-by-Step Information

Let’s illustrate how you can use the Z-chart with an instance. Suppose we have now a usually distributed dataset with a imply of fifty and a typical deviation of 10. We need to discover the chance of observing a price lower than 65.

1. Calculate the Z-score:

   Z = (65 – 50) / 10 = 1.5

2. Find the Z-score on the Z-chart: Discover the row equivalent to 1.5 and the column equivalent to 0.00 (the hundredths place of the Z-score).

3. Discover the chance: The intersection of the row and column provides the cumulative chance. For Z = 1.50, the chance is roughly 0.9332.

This implies there is a 93.32% chance of observing a price lower than 65 on this dataset.

Purposes of the Z-Chart and Z-scores:

The Z-chart and Z-scores have wide-ranging functions in numerous fields:

• Speculation Testing: Z-tests are used to match inhabitants means or proportions. The Z-score helps decide the importance of the outcomes.

• Confidence Intervals: Z-scores are essential in developing confidence intervals, which give a spread of values more likely to include the true inhabitants parameter.

• Course of Management: In high quality management, Z-scores are used to observe processes and establish outliers.

• Percentile Calculations: The Z-chart can be utilized to find out the worth equivalent to a particular percentile in a standard distribution. For instance, discovering the ninetieth percentile includes discovering the Z-score equivalent to a cumulative chance of 0.90 after which changing it again to the unique scale utilizing the components: X = μ + Zσ.

• Knowledge Standardization and Comparability: Z-scores permit for the comparability of knowledge from completely different datasets with completely different scales. By standardizing the info, we are able to evaluate the relative positions of knowledge factors inside their respective distributions.

• Danger Administration and Finance: In finance, Z-scores are used to evaluate the creditworthiness of debtors and to mannequin market dangers.

Limitations of the Z-Chart and Regular Distribution Assumptions:

Whereas the traditional distribution is broadly relevant, it is essential to acknowledge its limitations:

• Assumption of Normality: The Z-chart is simply relevant if the info follows a standard distribution. If the info is considerably skewed or has heavy tails, utilizing the Z-chart can result in inaccurate outcomes. Assessments just like the Shapiro-Wilk check can be utilized to evaluate normality.

• Inhabitants Parameters: The Z-score calculation requires data of the inhabitants imply and commonplace deviation. If these parameters are unknown, the t-distribution and t-tests may be extra applicable.

• Small Pattern Sizes: For small pattern sizes, the t-distribution is usually most popular over the traditional distribution.

• Discrete Knowledge: The conventional distribution is for steady information. For discrete information, different chance distributions could also be extra appropriate.

Past the Fundamentals: Superior Purposes and Extensions

The Z-chart supplies a basis for understanding and dealing with regular distributions. Nevertheless, extra superior statistical strategies construct upon these basic ideas:

• Central Restrict Theorem: This theorem states that the sampling distribution of the imply approaches a standard distribution because the pattern dimension will increase, whatever the underlying inhabitants distribution. This permits us to make use of Z-scores and the Z-chart even when coping with non-normal populations, supplied the pattern dimension is sufficiently massive.

• Multivariate Regular Distribution: This extends the idea of the traditional distribution to a number of variables, permitting for the evaluation of relationships between variables.

• Non-parametric Strategies: When the idea of normality is violated, non-parametric strategies, which do not depend on the normality assumption, can be utilized.

Conclusion:

The Z-chart is a useful instrument for working with usually distributed information. Understanding its functions and limitations is essential for correct statistical evaluation throughout numerous disciplines. By mastering the usage of Z-scores and the Z-chart, researchers and practitioners can acquire precious insights from their information, make knowledgeable selections, and contribute to developments of their respective fields. Whereas the Z-chart supplies a robust technique for analyzing usually distributed information, it is vital to recollect to evaluate the assumptions of normality and think about various approaches when essential. The cautious utility of the Z-chart, coupled with a crucial understanding of its limitations, ensures the sturdy and dependable interpretation of statistical outcomes.

Closure

Thus, we hope this text has supplied precious insights into Navigating the Regular Distribution: A Complete Information to the Z-Chart. We thanks for taking the time to learn this text. See you in our subsequent article!