Understanding And Making use of The X-Bar Chart Higher Management Restrict Components: A Complete Information

Understanding and Making use of the X-Bar Chart Higher Management Restrict Components: A Complete Information

Associated Articles: Understanding and Making use of the X-Bar Chart Higher Management Restrict Components: A Complete Information

Introduction

On this auspicious event, we’re delighted to delve into the intriguing matter associated to Understanding and Making use of the X-Bar Chart Higher Management Restrict Components: A Complete Information. Let’s weave attention-grabbing info and supply recent views to the readers.

Understanding and Making use of the X-Bar Chart Higher Management Restrict Components: A Complete Information

The X-bar chart, a cornerstone of Statistical Course of Management (SPC), is a strong instrument for monitoring the common of a course of over time. Its effectiveness hinges on precisely establishing management limits, which outline the boundaries inside which the method is taken into account to be in a state of statistical management. This text delves deeply into the system for the higher management restrict (UCL) of an X-bar chart, explaining its derivation, software, and nuances. We’ll discover numerous situations, deal with widespread misconceptions, and spotlight the crucial function of information integrity in correct UCL calculation.

The Basis: Understanding Statistical Management and Course of Variation

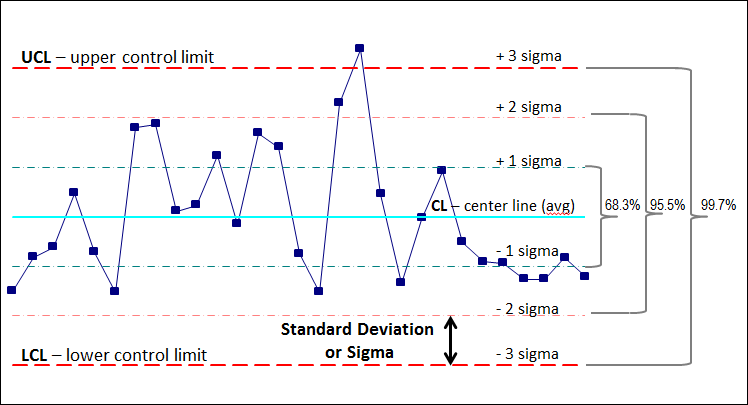
Earlier than diving into the system itself, it is essential to know the underlying rules. A course of is taken into account statistically managed when its variation is solely as a consequence of widespread trigger variation – inherent, random fluctuations which are unavoidable inside the system. Particular trigger variation, however, represents unpredictable, assignable causes that disrupt the method and result in deviations outdoors the anticipated vary. The X-bar chart goals to detect these particular causes by monitoring the common of subgroups sampled from the method.

The UCL, together with the decrease management restrict (LCL) and the central line (CL), visually characterize the anticipated vary of variation for a statistically managed course of. Factors plotted outdoors these limits recommend the presence of particular trigger variation, warranting investigation and corrective motion.

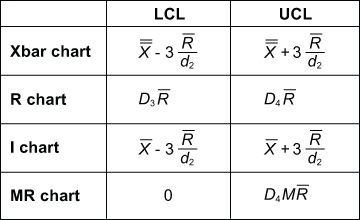
Deriving the X-bar Chart Higher Management Restrict Components

The UCL for an X-bar chart is calculated utilizing the next system:

UCL = X̄ + A₂R̄

The place:

• UCL: The higher management restrict.
• X̄: The general common of all subgroup averages. That is calculated by summing the averages of all subgroups and dividing by the variety of subgroups.
• A₂: A management chart fixed that depends upon the subgroup dimension (n). These constants are available in statistical tables or software program packages. The worth of A₂ accounts for the variability inside subgroups and the uncertainty in estimating the method commonplace deviation.
• R̄: The common vary of all subgroups. That is calculated by summing the ranges of all subgroups and dividing by the variety of subgroups. The vary is solely the distinction between the biggest and smallest values inside every subgroup.

Let’s break down every element:

• X̄ (X-bar): This represents the grand common of the method. It is a measure of the central tendency of the info throughout all subgroups. A steady course of may have a comparatively constant X̄ over time.

• R̄ (R-bar): This represents the common vary of variation inside the subgroups. It is a measure of the dispersion or unfold of the info inside every subgroup. A smaller R̄ signifies much less within-subgroup variation.

• A₂: This fixed is essential as a result of it adjusts the management limits primarily based on the subgroup dimension. Bigger subgroup sizes (n) typically result in smaller A₂ values, reflecting the elevated precision in estimating the method commonplace deviation with extra knowledge factors inside every subgroup. Utilizing an incorrect A₂ worth will result in inaccurate management limits and doubtlessly flawed interpretations. Tables of A₂ values are available in statistical high quality management handbooks and software program.

Illustrative Instance:

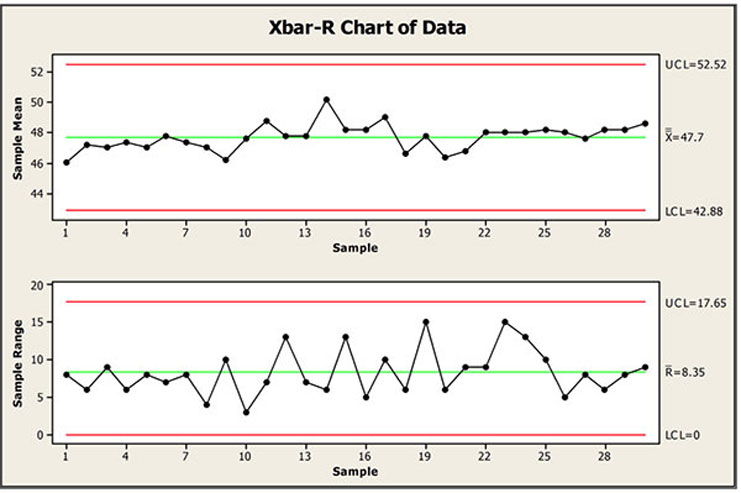
Let’s contemplate a producing course of the place we acquire 25 subgroups of dimension 5 (n=5). After calculating the common of every subgroup and the vary of every subgroup, we get hold of the next:

• X̄ = 100 (the grand common of all subgroup averages)
• R̄ = 10 (the common vary of all subgroups)
• From a management chart fixed desk, A₂ for n=5 is 0.577.

Utilizing the system:

UCL = X̄ + A₂R̄ = 100 + (0.577 * 10) = 105.77

Subsequently, the higher management restrict for this X-bar chart is 105.77. Any subgroup common exceeding this worth would sign a possible out-of-control situation.

Different Components Utilizing Normal Deviation:

Whereas the R̄ technique is usually used as a consequence of its simplicity, another strategy makes use of the usual deviation (σ) of the subgroups. The system on this case is:

UCL = X̄ + 3σ/√n

The place:

• σ: The estimated commonplace deviation of the method. This may be calculated utilizing the common vary (R̄) or immediately from the subgroup knowledge. A typical approximation is σ ≈ R̄/d₂, the place d₂ is one other management chart fixed depending on the subgroup dimension (n).

This system makes use of the idea of 3-sigma limits, a extensively accepted conference in SPC. The three-sigma limits embody roughly 99.73% of the info factors for a usually distributed course of. Nonetheless, the R̄ technique is commonly most popular for its simplicity and robustness to deviations from normality.

Assumptions and Concerns:

The accuracy and reliability of the UCL calculation rely upon a number of assumptions:

• Information Independence: The subgroups ought to be unbiased of one another. Which means that the measurements inside one subgroup mustn’t affect the measurements in one other subgroup.
• Information Normality: Whereas the X-bar chart is comparatively strong to deviations from normality, significantly with bigger subgroup sizes, important departures from normality can have an effect on the accuracy of the management limits. Normality exams will be carried out to evaluate the info distribution.
• Fixed Course of Variance: The method variance ought to stay comparatively fixed over time. If the variance modifications considerably, the management limits might develop into inaccurate.
• Subgroup Dimension: The selection of subgroup dimension (n) is crucial. Bigger subgroups present extra exact estimates of the method common and variance, however they could be extra time-consuming and costly to gather. A stability should be struck between precision and practicality.
• Rational Subgrouping: Subgroups ought to be chosen in a method that captures the inherent variability of the method. Cautious consideration ought to be given to components which may affect the method output.

Software program and Instruments:

Quite a few statistical software program packages (e.g., Minitab, JMP, R) and specialised SPC software program supply instruments for routinely calculating management limits, plotting X-bar charts, and performing associated analyses. These instruments usually present extra options like functionality evaluation, run chart evaluation, and computerized detection of out-of-control factors.

Conclusion:

The correct calculation and interpretation of the X-bar chart higher management restrict are important for efficient course of monitoring and enchancment. Understanding the system, its underlying assumptions, and the potential pitfalls is essential for making knowledgeable choices primarily based on the management chart outcomes. By fastidiously deciding on subgroup sizes, guaranteeing knowledge integrity, and utilizing acceptable statistical instruments, practitioners can successfully make the most of the X-bar chart to establish and deal with particular trigger variation, resulting in improved course of stability and diminished variability. Keep in mind to at all times seek the advice of related statistical sources and contemplate looking for professional recommendation when coping with complicated knowledge or crucial purposes. The ability of the X-bar chart lies in its simplicity and effectiveness, however its correct software requires an intensive understanding of its underlying rules and limitations.

Closure

Thus, we hope this text has supplied worthwhile insights into Understanding and Making use of the X-Bar Chart Higher Management Restrict Components: A Complete Information. We recognize your consideration to our article. See you in our subsequent article!