X-bar And R Chart: A Complete Solved Instance With Detailed Rationalization
X-bar and R Chart: A Complete Solved Instance with Detailed Rationalization
Associated Articles: X-bar and R Chart: A Complete Solved Instance with Detailed Rationalization
Introduction
With nice pleasure, we’ll discover the intriguing subject associated to X-bar and R Chart: A Complete Solved Instance with Detailed Rationalization. Let’s weave attention-grabbing data and provide recent views to the readers.
Desk of Content material
X-bar and R Chart: A Complete Solved Instance with Detailed Rationalization

Statistical Course of Management (SPC) is an important software for monitoring and bettering manufacturing processes. One of the broadly used SPC charts is the X-bar and R chart, designed for monitoring the central tendency (common) and the variability (vary) of a course of. This text presents an in depth, solved instance demonstrating the creation and interpretation of X-bar and R charts, offering a complete understanding of their software.
Understanding X-bar and R Charts
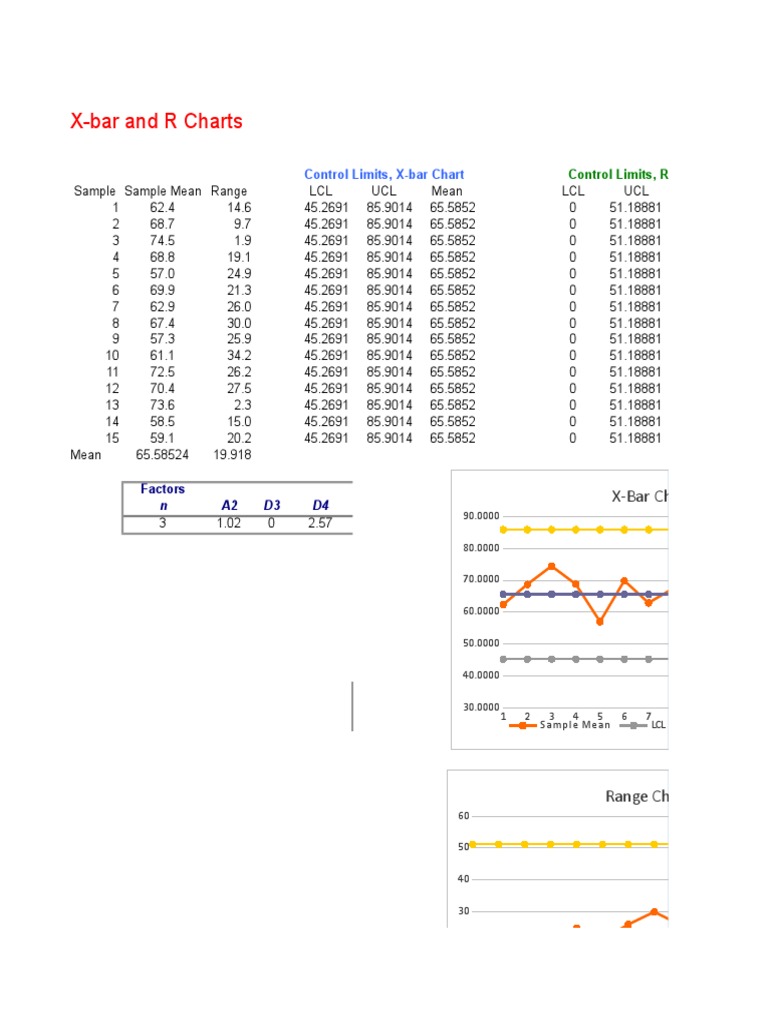
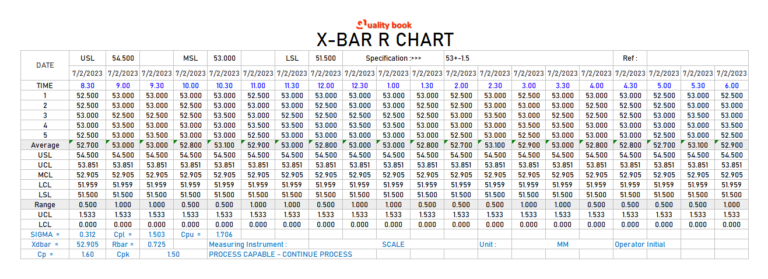
The X-bar chart tracks the typical (imply) of a course of attribute over time. It helps establish shifts within the course of imply, indicating potential issues like machine malfunction or uncooked materials inconsistencies. The R chart, then again, screens the vary (distinction between the biggest and smallest values) inside subgroups of information. It helps detect modifications within the course of variability, signaling points corresponding to elevated inconsistency or operator error. These charts are sometimes used collectively as a result of modifications in variability usually precede modifications within the common.
Assumptions for X-bar and R Charts
The efficient software of X-bar and R charts depends on a number of assumptions:
- Knowledge are steady: The attribute being measured ought to be a steady variable (e.g., weight, size, temperature).
- Knowledge are usually distributed: Whereas not strictly required, normality improves the accuracy of the management limits. For bigger pattern sizes (n>10), the Central Restrict Theorem helps mitigate the affect of non-normality.
- Subgroups are impartial: Knowledge factors inside subgroups ought to be associated, however subgroups ought to be impartial of one another. For instance, samples taken at completely different instances of the day can be thought-about impartial subgroups.
- Course of is steady (in management) when the chart is created: The preliminary information used to ascertain the management limits ought to characterize the method’s inherent variability. Out-of-control factors ought to be investigated and eliminated earlier than establishing management limits.
- Fixed variability: The method variance ought to stay comparatively fixed over time.
Solved Instance: Monitoring the Diameter of a Manufactured Half
Let’s take into account a producing course of producing cylindrical elements. The essential attribute is the diameter, measured in millimeters. We gather 25 subgroups, every containing 5 samples (n=5). The info are offered within the desk under:
| Subgroup | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Subgroup Imply (X-bar) | Subgroup Vary (R) |
|---|---|---|---|---|---|---|---|
| 1 | 24.98 | 25.02 | 25.00 | 24.99 | 25.01 | 25.00 | 0.04 |
| 2 | 25.01 | 24.97 | 25.03 | 25.00 | 24.99 | 25.00 | 0.06 |
| 3 | 24.99 | 25.01 | 25.02 | 24.98 | 25.00 | 25.00 | 0.04 |
| 4 | 25.02 | 25.00 | 24.99 | 25.01 | 25.03 | 25.01 | 0.04 |
| 5 | 24.98 | 24.99 | 25.00 | 25.02 | 25.01 | 25.00 | 0.04 |
| … | … | … | … | … | … | … | … |
| 25 | 25.03 | 24.98 | 25.01 | 25.00 | 24.99 | 25.00 | 0.05 |
(Be aware: The "…" represents the info for subgroups 6 by way of 24. For brevity, the total dataset just isn’t included right here, however the calculations will likely be proven utilizing abstract statistics.)
Step 1: Calculate the Common of Subgroup Means (X-double bar) and the Common Vary (R-bar)
After gathering all the info, calculate the typical of the subgroup means (X-double bar) and the typical of the subgroup ranges (R-bar). Let’s assume, for this instance, that after calculating the means and ranges for all 25 subgroups:
- X-double bar (total common of means) = 25.002
- R-bar (common vary) = 0.045
Step 2: Decide Management Limits utilizing Management Chart Constants
To find out the management limits, we’d like management chart constants. These constants depend upon the subgroup dimension (n). For n=5, the constants are available in statistical tables or software program packages:
- A2 (for X-bar chart) = 0.577
- D3 (for R chart) = 0
- D4 (for R chart) = 2.115
Step 3: Calculate Management Limits for the X-bar Chart
The management limits for the X-bar chart are calculated as follows:
- Higher Management Restrict (UCL) for X-bar = X-double bar + A2 R-bar = 25.002 + 0.577 0.045 = 25.030
- Central Line (CL) for X-bar = X-double bar = 25.002
- Decrease Management Restrict (LCL) for X-bar = X-double bar – A2 R-bar = 25.002 – 0.577 0.045 = 24.974
Step 4: Calculate Management Limits for the R Chart
The management limits for the R chart are calculated as follows:
- Higher Management Restrict (UCL) for R = D4 R-bar = 2.115 0.045 = 0.095
- Central Line (CL) for R = R-bar = 0.045
- Decrease Management Restrict (LCL) for R = D3 R-bar = 0 0.045 = 0
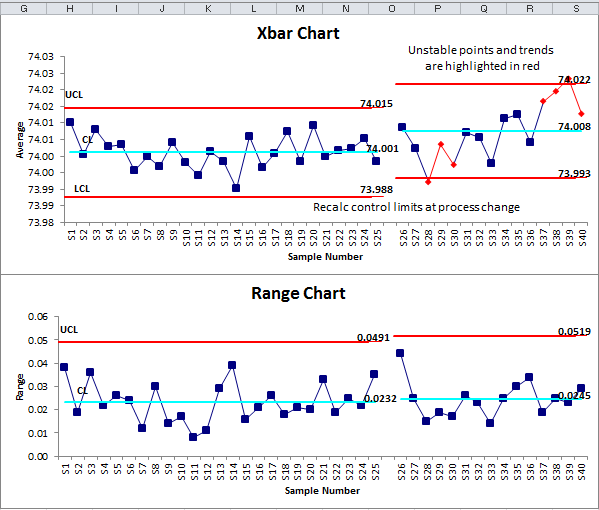
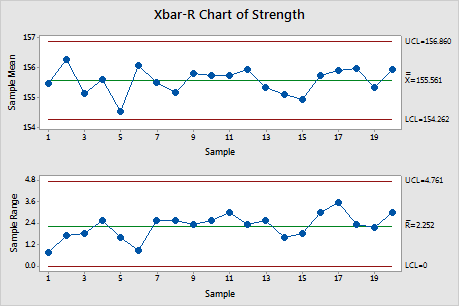
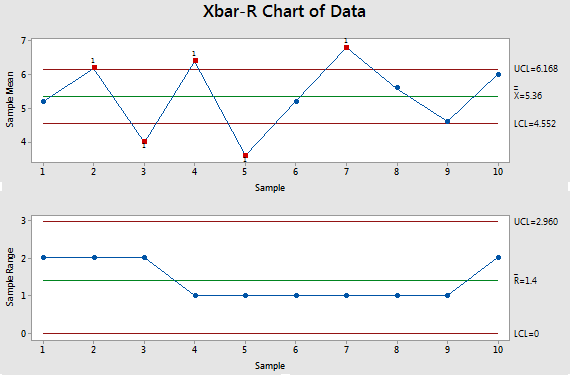
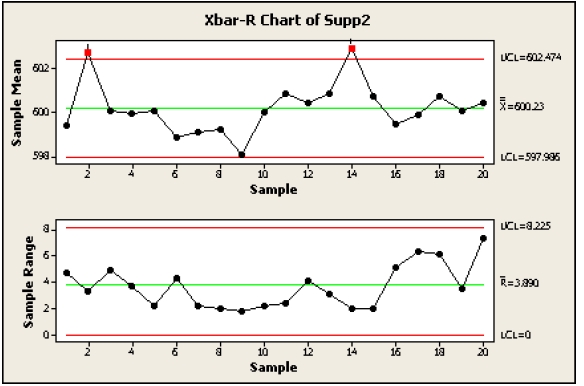
Step 5: Plot the Knowledge and Management Limits
Now, plot the subgroup means (X-bar) on the X-bar chart and the subgroup ranges (R) on the R chart. The management limits calculated above are plotted as horizontal strains on every chart.
Step 6: Interpret the Charts
Study the charts for any factors that fall outdoors the management limits or exhibit non-random patterns. Factors outdoors the management limits point out potential course of issues requiring investigation. Non-random patterns, corresponding to developments or cycles, additionally counsel course of instability.
Instance Interpretation:
Let’s assume that in our instance, one subgroup’s imply falls above the UCL for the X-bar chart, and one other subgroup’s vary falls above the UCL for the R chart. This is able to point out potential points. The investigation would possibly contain checking the machine settings, inspecting the uncooked supplies, or reviewing operator procedures for these particular subgroups. If the out-of-control factors are as a consequence of assignable causes (particular identifiable elements), these causes ought to be eradicated. The charts ought to then be re-created utilizing solely the info from the in-control intervals.
Conclusion:
The X-bar and R charts present a strong software for monitoring course of efficiency. By monitoring each the central tendency and variability, these charts assist establish potential issues early, stopping the manufacturing of non-conforming merchandise and bettering total course of effectivity. This instance demonstrates the step-by-step process for establishing and deciphering these charts, highlighting the significance of understanding the underlying assumptions and deciphering the outcomes fastidiously. Keep in mind that the success of SPC depends not solely on the right software of statistical methods but additionally on efficient investigation and corrective actions when out-of-control situations are detected. Additional evaluation, corresponding to functionality evaluation, will be carried out as soon as the method is demonstrated to be in management. Software program packages devoted to statistical course of management considerably simplify the calculations and plotting concerned in creating and analyzing these charts.


Closure
Thus, we hope this text has supplied invaluable insights into X-bar and R Chart: A Complete Solved Instance with Detailed Rationalization. We hope you discover this text informative and helpful. See you in our subsequent article!